
题目列表(包括答案和解析)
7、一个半径为R的球与体对角线长为l的正方体的六个面都相切,则R与l的关系是 ( )
A. l=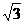 R B. l=2
R B. l=2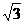 R C. l=2R D. 2R=
R C. l=2R D. 2R=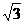 l.
l.
6、已知函数f(x)=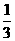 x3+
x3+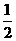 x2+tx是R上的单调增函数,则t的值可能是 ( )
x2+tx是R上的单调增函数,则t的值可能是 ( )
A. t=1 B. t=0 C. t = -1 D. 不存在.
5、已知球面上两点的球面距离为1cm,过这两点的球半径所成的角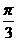 ,则球的半径为
,则球的半径为
( )
A. 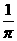 cm B.
cm B. 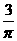 cm C. πcm D. 3πcm .
cm C. πcm D. 3πcm .
4、已知直线l,m,n及平面α,下列命题中的假命题是 ( )
A.若l∥m,m∥n,则l∥n B.若l⊥α,m∥α,则l⊥m
C.若l⊥m,m∥n,则l⊥n D.若l∥α,n∥α,则l∥n.
3、高二年级12个班共有580人,要采用分层抽样的方法从高二年级的全体学生中抽取一个容量为60的样本,已知某班有58名学生,那么从该班抽取的学生数是 ( )
A. 5 B. 6 C. 10 D. 12.
2、在棱长为1的正方体ABCD-A1B1C1D1中,异面直线AB与CD1之间的距离是 ( )
A. 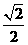 B.
B.
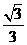 C. 1 D.
C. 1 D. 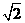 .
.
1、函数f(x)=2的导数是 ( )
A. 2 B. 1 C . 0 D. 2x.
(19)(本题满分12分)
解下列不等式:
(Ⅰ)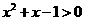 ;
(Ⅱ)
;
(Ⅱ)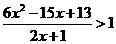 .
.
(20)(本题满分12分)
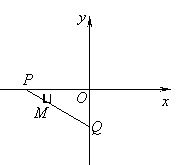
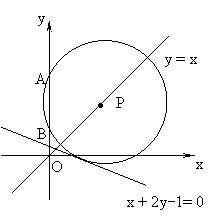 如图所示,圆心P在直线
如图所示,圆心P在直线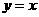 上,且与直线
上,且与直线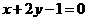 相切的圆,截
相切的圆,截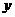 轴的上半轴所得的弦
轴的上半轴所得的弦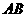 长为2,求此圆的方程.
长为2,求此圆的方程.
(21)(本题满分14分)
已知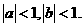
(Ⅰ)求证: 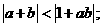
(Ⅱ)若不等式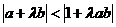 恒成立,求实数
恒成立,求实数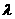 的取值范围。
的取值范围。
(22) (本题满分14分)
在平面直角坐标系中,长度为6的线段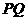 的一个端点
的一个端点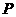 在射线
在射线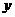 =0(
=0(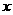 ≤0)上滑动,另一端点
≤0)上滑动,另一端点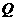 在射线
在射线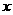 =0(
=0(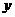 ≤0) 上滑动,点
≤0) 上滑动,点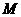 在线段
在线段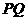 上,且
上,且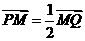 .
.
(Ⅰ)求点M的轨迹方程;
(Ⅱ)若点M的轨迹与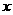 轴、
轴、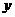 轴分别交于点A、B,求四边形OAMB面积的最大值.
轴分别交于点A、B,求四边形OAMB面积的最大值.
(23) (本题满分14分)
已知圆锥曲线的一个焦点为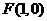 , 对应这个焦点的准线方程为
, 对应这个焦点的准线方程为 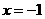 , 且这条曲线经过点
, 且这条曲线经过点 .
.
(Ⅰ)求此圆锥曲线的方程;
(Ⅱ)设直线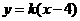 与圆锥曲线相交于A、B两点,与
与圆锥曲线相交于A、B两点,与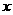 轴交于点P,O为坐标原点,若
轴交于点P,O为坐标原点,若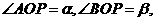 求
求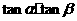 的值.
的值.
宿迁市2005-2006学年度第一学期期末考试
(13)直线 的倾斜角为 ▲ .
的倾斜角为 ▲ .
(14)若直线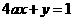 与直线
与直线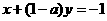 互相垂直,则
互相垂直,则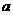 = ▲ .
= ▲ .
(15)以双曲线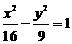 的中心为顶点,左焦点为焦点的抛物线方程是__▲ _.
的中心为顶点,左焦点为焦点的抛物线方程是__▲ _.
(16)一段长为L米的篱笆围成一个一边靠墙的矩形菜园,则这个菜园的最大面积是 ▲ .
(17)已知P是双曲线 上一动点,则线段OP(O为坐标原点)的中点M的轨迹方程是 ▲ .
上一动点,则线段OP(O为坐标原点)的中点M的轨迹方程是 ▲ .
(18)设关于x的不等式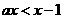 的解集为A,若
的解集为A,若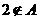 ,则实数
,则实数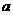 的取值范围
的取值范围
是 ▲ .
(1)直线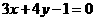 的斜率是 ( )
的斜率是 ( )
(A)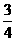 (B)
(B)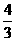 (C)
(C) 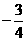 (D)
(D) 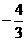
(2)不等式“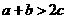 ”成立的一个充分条件是( )
”成立的一个充分条件是( )
(A) (B)
(B)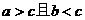
(C)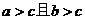 (D)
(D)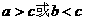
(3)双曲线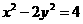 的离心率是 ( )
的离心率是 ( )
(A) 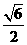 (B)
(B) 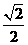 (C)
(C)
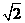 (D)
(D)
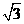
(4)已知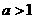 ,则
,则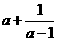 的最小值是 ( )
的最小值是 ( )
(A)2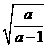 (B)
(B)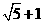 (C)2
(D)3
(C)2
(D)3
(5)直线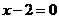 与
与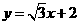 的夹角是 ( )
的夹角是 ( )
(A)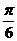 (B)
(B)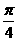 (C)
(C)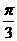 (D)
(D)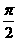
(6)若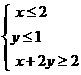 , 则线性目标函数
, 则线性目标函数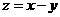 的取值范围是 ( )
的取值范围是 ( )
(A) [ -2,-1 ] (B) [ -2,1 ] (C) [ -1,2] (D) [ 1,2 ]
(7)与双曲线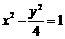 有共同的渐近线,且过点(2,2)的双曲线方程是( )
有共同的渐近线,且过点(2,2)的双曲线方程是( )
(A)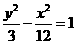 (B)
(B)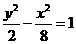
(C)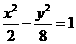 (D)
(D)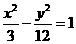
(8)不等式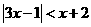 的解集是 ( )
的解集是 ( )
(A)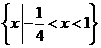 (B)
(B) 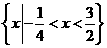
(C) 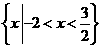 (D)
(D)
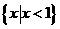
(9)若椭圆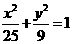 上 的一点P到左准线的距离为
上 的一点P到左准线的距离为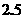 ,则点P到右焦点的距离是(
)
,则点P到右焦点的距离是(
)
(A)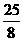 (B)
(B)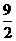 (C)
(C)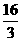 (D)8
(D)8
(10)若直线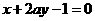 与直线
与直线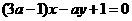 平行,则
平行,则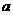 的值是 ( )
的值是 ( )
(A)0 (B)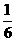 (C)
(C)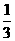 (D)
(D)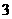
(11)设经过双曲线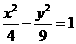 左焦点的直线
左焦点的直线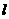 与双曲线交于点A、B,若
与双曲线交于点A、B,若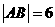 ,则这样的直线有 ( )
,则这样的直线有 ( )
(A)1 条 (B)2条 (C)3条 (D)4条
(12)设点 的左准线上,过点
的左准线上,过点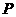 且方向为
且方向为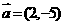 的光线经直线
的光线经直线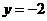 反射后通过椭圆的左焦点,则这个椭圆的方程是( )
反射后通过椭圆的左焦点,则这个椭圆的方程是( )
(A)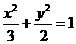 (B)
(B)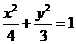
(C)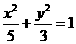 (D)
(D)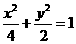
第二卷(非选择题共90分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com