
题目列表(包括答案和解析)
19. (本小题满分12分)
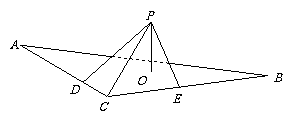 在
在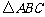 中,
中,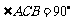 ,平面
,平面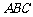 外有一点
外有一点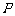 ,
,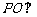 平面
平面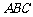 ,垂足为
,垂足为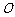 .已知
.已知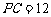 ,点
,点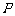 到直线
到直线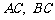 的距离
的距离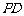 和
和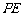 都为
都为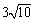 .求:
.求:
(Ⅰ) 点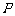 到平面
到平面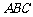 的距离;
的距离;
(Ⅱ) 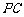 与平面
与平面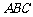 所成角的大小.
所成角的大小.
18. (本小题满分12分)
用铁丝制作一个正三棱柱形容器的框架,框架的总长度为18 m.
(Ⅰ)把正三棱柱形容器的体积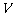 (m3)表示成底面边长
(m3)表示成底面边长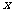 (m)的函数,并写出相应的定义域;
(m)的函数,并写出相应的定义域;
(Ⅱ)当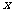 为何值时,容器的体积最大?求出它的最大值.
为何值时,容器的体积最大?求出它的最大值.
17.
 (本小题满分12分)
(本小题满分12分)
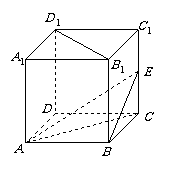
在正方体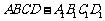 中,
中,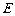 为棱
为棱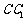 的中点.
的中点.
(Ⅰ) 求证: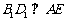 ;
;
(Ⅱ) 求二面角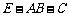 的正切值.
的正切值.
16.
在平面几何中有勾股定理:“设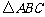 的两边
的两边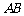 、
、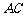 互相垂直,则
互相垂直,则
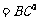 ”;拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面积和底面积的关系,可以得到的正确结论是:“设三棱锥
”;拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面积和底面积的关系,可以得到的正确结论是:“设三棱锥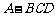 的三个侧面
的三个侧面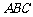 、
、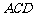 、
、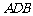 两两相互垂直,则 ▲ ”.
两两相互垂直,则 ▲ ”.
15.
已知二面角角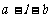 的大小为
的大小为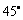 ,半平面
,半平面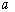 内有一条直线
内有一条直线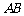 ,
,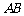 与棱
与棱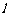 所成的角为
所成的角为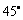 ,则
,则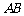 与平面
与平面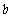 所成的角为 ▲ .
所成的角为 ▲ .
14.
函数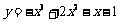 的单调递增区间为 ▲ .
的单调递增区间为 ▲ .
13.
空间向量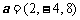 与
与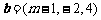 平行,则
平行,则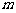 为 ▲ .
为 ▲ .
12.
已知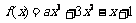 在
在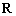 上是减函数,则
上是减函数,则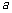 的取值范围为
的取值范围为
(A) 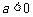 (B)
(B) 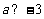 (C)
(C) 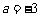 (D)
(D) 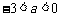
第Ⅱ卷(非选择题 共90分)
11.
四面体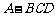 中,
中,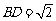 ,其余棱长均为1,则二面角
,其余棱长均为1,则二面角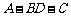 的大小为
的大小为
(A) 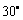 (B)
(B) 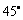 (C)
(C) 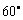 (D)
(D) 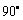
10.
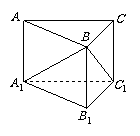 如图,直三棱柱
如图,直三棱柱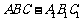 的侧面
的侧面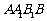 是边长为5 的正方形,若
是边长为5 的正方形,若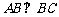 ,
,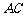 与
与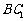 所成的角为
所成的角为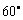 ,则
,则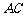 长为
长为
(A) 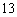 (B)
(B) 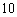
(C) 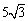 (D)
(D) 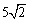
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com