23．(本小题满分15分)已知函数(、)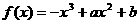

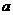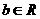(1)　　　 若函数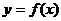的图象切x轴于点(2，0)，求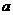、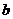的值；

(2)　　　 设函数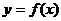(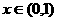)的图象上任意一点的切线的斜率为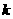，试求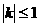的充要条件；

(3)　 若函数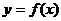的图象上任意不同的两点的连线的斜率小于1，求证：＜．

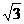22. (本小题满分15分)已知函数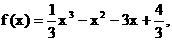 直线l : .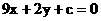

(1) 求证: 直线l与函数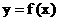的图像不相切;

(2) 若当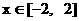时, 函数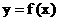的图像在直线l的下方, 求c的范围.

21．(本题满分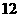分)设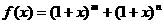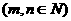，若其展开式中关于x的一次项系数的和为11，试问m、n为何值时，含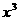项的系数和最小，这个最小值是多少？

20、(本题满分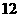分)如图，直二面角D-AB-E中，四边形ABCD

是边长为2的正方形，AE=EB，F为CE上的点，且BF⊥平面ACE.

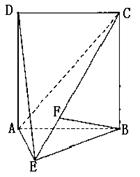(1)求证AE⊥平面BCE；

(2)求二面角B-AC-E的平面角的正弦值；

(3)求点D到平面ACE的距离.

19.(本小题满分12分)

　 在一次军事演习中，某军同时出动了甲、乙、丙三架战斗机对一军事目标进行轰炸，已知甲击中目标的概率是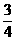；甲、丙同时轰炸一次，目标未被击中的概率为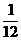；乙、丙同时轰炸一次，都击中目标的概率是.

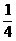　 (1)求乙、丙各自击中目标的概率；　 (2)求目标被击中的概率.

18．甲、乙两人玩猜数字游戏，先由甲心中任想一个数字，记为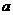，再由乙猜甲刚才所想的数字，把乙猜的数字记为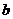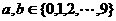，，若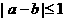，就称甲乙“心有灵犀”。现任意找两人玩这个游戏，得出他们“心有灵犀”的概率为_______.

17．函数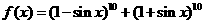的最大值是________。

16．一块各面均涂有红漆的正方体被锯成27个同样大小的正方体，若将这些小正方体搅混在一起，则任取出的一个正方体两面均涂有红漆的概率是　　　　　　　 。

15. 抛物线y=x²上P点切线和直线3x-y+1=0的交角为45⁰，则点P坐标为__________。

14．有一个正四棱锥，它的底面边长与侧棱长均为a，现用一张正方形包装纸将其完全包住(不能裁剪纸，但可以折叠)，那么包装纸的最小边长应为