
题目列表(包括答案和解析)
108、解:(1)设双曲线方程为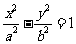
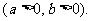
由已知得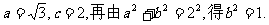
故双曲线C的方程为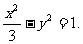
(2)将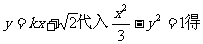
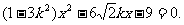
由直线l与双曲线交于不同的两点得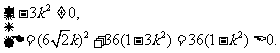
即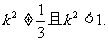 ① 设
① 设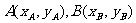 ,则
,则
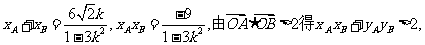
而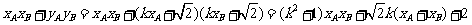
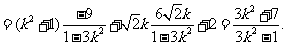
于是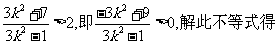
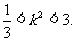 ②
②
由①、②得 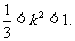
故k的取值范围为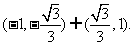
翰林汇
翰林汇
107、 解:双曲线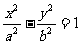 (a>0,b>0),中心(0,0),c2=a2+b2,
(a>0,b>0),中心(0,0),c2=a2+b2,
左焦点F1(-1,0),右焦点F2(c,0)
圆的方程为(x-c)2+y2=c2由题意,PF1为圆的切线,∴PF1⊥PF2,
∴|PF1|2+|PF2|2=|F1F2|2.(1)又点P在双曲线上,∴|PF1|-|PF2|=2
又|PF2|是圆的半径,∴|PF2|=c,
|PF1|=2a+c,|F1F2|=2c,代入(1)式,得(2a+c)2+c2=(2c)2,
4a2+4ac-2c2=0,∴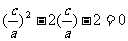 .
.
∴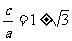 ,又e>1,∴e=
,又e>1,∴e=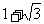 .
.
105、 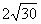 翰林汇
106、
翰林汇
106、 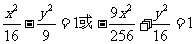 .翰林汇
.翰林汇
103、 提示:应用正弦定理及比例的性质. 翰林汇104、 略
102、 略解.记∠MAX=α,∠MBX=β,则0<α<β<900.
由对称性∠MNA= 2α,∠MBN=2β,
设M(x1,y1)(x1>0,y1>0),则x12-y12=a2.
tgα=tg∠MAX=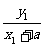 tgβ=∠MBN=
tgβ=∠MBN=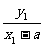 ,
,
∴tgα·tgβ=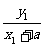 ·
·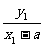 =
=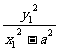 =1.∴tgα=tgβ=tg(900-β).
=1.∴tgα=tgβ=tg(900-β).
∵0<900-β<900,0<α<900.∴α=900-β.
由此,可得结论,∠MAN+∠MBN=1800.翰林汇
101、 解:M: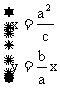 ,M(
,M(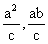 ),F(c,0),
),F(c,0),
KMF=-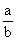 ,∴MF与渐近线y=
,∴MF与渐近线y=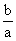 x垂直。
x垂直。
翰林汇
99、 略
翰林汇100、 定值为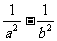 .提示:选择中心为极点的极坐标系.翰林汇
.提示:选择中心为极点的极坐标系.翰林汇
98、 证明: 若直线l不与x轴垂直,
则可设l的方程为y=kx+m, 代入双曲线方程b2x2-a2y2-a2b2=0,并整理得
(b2-a2k2)x2-2a2kmx-a2(m2+b2)=0,
设A(x1,y1),D(x2,y2),
则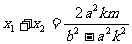 . 再将y=kx+m代入双曲线渐近线方程, 得b2x2-a2y2=0,并整理得(b2-a2k2)x2-2a2kmx-a2m2=0,
. 再将y=kx+m代入双曲线渐近线方程, 得b2x2-a2y2=0,并整理得(b2-a2k2)x2-2a2kmx-a2m2=0,
设B(x3,y3),C(x4,y4),则 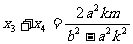 . ∴x1+x2=x3+x4.
. ∴x1+x2=x3+x4.
这说明线段AD的中点和线段BC的中点重合, 故|AB|=|CD|.翰林汇
93、提示:设双曲线方程为b2x2-a2y2=a2b2,则渐近线方程为b2x2-a2y2=0,再设直线方程,利用韦达定理证明线段AB与CD的中点重合.
翰林汇94、 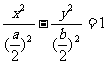 离心率都为
离心率都为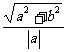 .
.
翰林汇95、 略 翰林汇96、 略翰林汇 97、 略翰林汇
89、 先证圆与准线相交, 然后得弧MN的弧度数为2arccos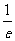 (e为双曲线离心率).
(e为双曲线离心率).
翰林汇90、 定值为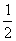 ab,a、b为双曲线的实半轴长、虚半轴长.
ab,a、b为双曲线的实半轴长、虚半轴长.
翰林汇91、 提示:在△F1MF2中使用余弦定理,并结合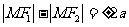
翰林汇92、 提示:类比于椭圆。翰林汇
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com