每题给出4个答案，其中只有一个是正确的，请把选出的答案编号填在上面的答题表中，否则不给分.

1、用α表示一个平面，l表示一条直线，则平面α内至少有一条直线与l

A、平行　　　　　　　　　 B、相交　　　　　　　　　 C、异面　　　　　　　　　 D、垂直

21、解:

(1)　　 连结MD,AC=BC,M为AB中点

所以CM⊥AB

又旋转前CD⊥AB,所在旋转后, CD⊥AD,CD⊥DB,且AD∩BD=D,所以CD⊥面ABD

又CM⊥AB,所以DM⊥AB(三垂线逆定理)

又CM∩DM=M,所以AB⊥面CMD

由已知DH⊥CM,所以DH⊥BC(三垂线定理)

(2)　　 取AC中点N, 连结MN,DN,

由M为AB中点,知MN∥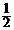BC,所以∠DMN为异面直线BC与MD所成的角.

(求∠DMN过程略) ∠DMN=60°

(3)　　 由已知DH⊥CM,又由(1)知DH⊥BC,而且CM∩BC=C

所以DH⊥面ABC,由已知H是垂足,即H是D在平面ABC上的射影

故DH的长为等于点D到平面ABC射影之间的距离.

(求DH的长略)则DH=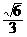

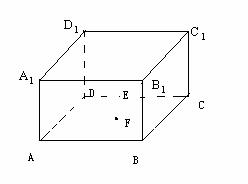
17、(1)与AA′垂直的棱有：

　AB、BC、CD、DA、A′B′、B′C′、C′D′、D′A′

(2)连结BC′，DB，DC′，在长方体中，有D′B′∥DB，由E、F为棱中点可知EF∥C′B，则可知∠DBC′即为所求的异面直线D′B′与EF所成的角，在△DBC′中，可求得：DB=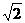，BC′=DC′=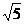，所以，cos∠DBC′=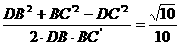

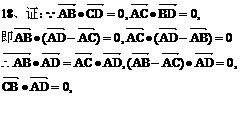
13、③、④ 　14、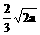　　 15、点P在平面AB₁C内 16、这个角的平分线

1、B，2、C，3、D，4、D，5、A，6、D 7、C 8、C 9、D10、D 11、C12、D

21.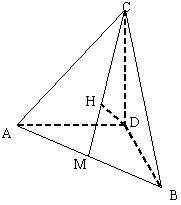已知等腰Rt△ABC中,∠ACB=90°,AC=2, 以AB边上的高CD为轴,把△ADC绕轴旋转至∠ADB=90°,并在AB上取中点M, 过D作DH⊥CM于H.

(1)　　 证明:DH⊥BC

(2)　　 求:异面直线BC与MD所成的角,

(3)　　 求:点D到平面ABC射影之间的距离.

19、如图，长方体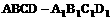中，E、F为面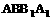上两点，过F在面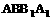上作直线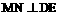，并写出作法

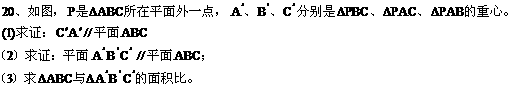
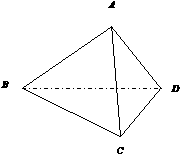
18、如图已知空间四边形ABCD中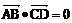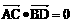， ，证明：.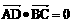

17、如图长方体中，AB=BC=1，AA′=2，E、F分别为棱中点。

(1)　　　 写出所有与AA′垂直的棱；

(2)　　　 求异面直线D′B′与EF所成角的余弦值。

16、经过一个角的顶点引这个角所在平面的斜线，如果它和已知角两边的夹角为锐角且相等，那么这条斜射线在在平面内的射影是