(18) 双曲线x²-my²=1(m>0)的右顶点为A、而B,C是双曲线左支上两点，若三角形为正三角形，则m的取值范围是 　　　　　　　　　

(19) 在三角形ABC中，A、B、C形对的边分别为a、b、c,B(-1,0),C(1,0),且2sinB=sinA,则点A的轨迹方程是　　　　　　　　　　　

(16) x,y满足4(x-2)²+y²=4，则y/x的最小值是(　 　)

A.2√3/2　　　　　　 B.-2√3/2　　　　　　 C.1　　　　　　 D.-1

(17) 对于任意n∈N，抛物线y=(n²+n)x-(2n+1)x+1与x轴交于两点A_n,B_n，以|A_nB_n|表示间的距离，则|A₁B₁|+|A₂B₂|+…+|A₂₀₀₀B₂₀₀₀|=(　 )

A .2000/1999　　　　 B. 1999/2000　　　　　 C.2001/2000　　　 D. 2000/2001

(13)求过点(3,0)离心率为√6/3的椭圆的标准方程.　　　　　 　　　　　　　　　　　　　　

(14)点(x,y)与定点F(c,0)的距离和它到直线l:x=a²/c的距离比是常数a/c(c>a>0)，，求点M的轨迹.

(15) 过抛物线y²=x的顶点任作互相垂直的玄OA与OB，求证直线AB必过定点.

高中期中数学试题(理.B卷)

时间约40分钟、满分50分

(11)两条直线3x+4y-12=0和6x+8y+11=0的距离是 　　　　　

(12) 设M(0,-5)和N(0,5),三角形PMN的周长为36，则顶点P的轨迹方程为　　　　　

(1)　　 直线l过原点及点(-1,-1),则它的倾斜角是　　　　　　　　　　　　　　　　 (　 )

A.π/4　　　　　　 B.5π/4　　　　　 C.π/4或5π/4　　　 D.-π/4

(2)　　 在x轴上截距为2，在y轴上截距为-2的直线方程是　　　　　　　　　　 (　 )

A.x/2+y/-2=1　　　 B.x/-2+y/2=1　 　　　C.x/-2+y/-2=1　　　　 D.x/2+y/2=1

(3)　　 直线ax+5y+2=0与直线x+2y+3=0互相垂直、则a的值为　　　　　　　　 (　 )

A.-6　　　　　　　 B.-8　　　　　　　 C-10　　　　　　　 D.10

(4)　　 巳知点(3,1)和点(-4,6)在直线3x-2y+a=0的两侧、则a的取值范围是　　　　 (　 )

A.a<7或a>24　　 B.a=7或a>24　　　 C.-7<a<24　　 　　D.-24<a<7

(5)　　 到两条坐标轴距离相等的动点轨迹方程为　　　　　　　　　　　　　　　 (　 )

Ay=x　　　　　　 B.Y=|x|　　　　　 C.y²=x² 　　　　　D.x²+y²=0

(6)　　 方程x²+y²-x+y+m=0表示一个圆、则　　　　　　　　　　　　　　　　　 (　 )

A.m≤2　　　　　 B.m<2　　　　　　 C.m<1/2　　　　　 D.m≤1

(7)　　 已知椭圆x²/25+y²/16=1上一个点P到其中一个焦点的距离为3、则P到另一个焦点的距离为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　 )

A.2　　　　　　 B.3　　　　　　 C.5　　　　　　　 D.7

(8)　　 双曲线3mx²-my²=3的一条准线为y=1/2、则m等于　　　　　　　　　　　 (　　 )

A.-1　　　　　　 B.1　　　　　　 　C,-9　　　　　　　 D.9

(9)　　 过点与抛物线y²=mx(m>0)只有一个公共点的直线的条数是　　　　　　　　 (　 )

A.1　　　　　　 B.2　　　　　　　 C3　　　　　　　 D.4

(10)设椭圆x²/a²+y²/b²=1(a>b>0)的离心率为e,焦距为2c则椭圆上一点P(x₀,y₀)到两个焦点的距离是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　 )

A.ex₀+c.　 ex₀-c　 B. ex₀+c .c-ex₀　　 C. a+ex_0. a-ex₀　　　 D. ex₀+a. ex₀-a

25．　　　　　 设f(x)=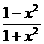

(i)　　　　　　 判断函数f(x)在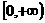上的单调性，并按单调性定义证明.

(ii)　　　　　 求f(x)的值域.

24．　　　　　 设f(x)是定义在实数集R上的函数，且对任何x₁，x₂∈R满足f(x₁+x₂)=f(x₁)+f(x₂)，求证f(0)=0，且f(x)是奇函数.

23．　　　　　 已知f(x)=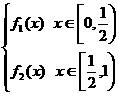,其中f₁(x)=-2(x-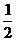)²+1,f₂(x)=-2x+2,

(i)　　　 画出y=f(x)的图象

(ii)　　 若x₀∈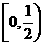，x₁=f(x₀)，f(x₁)=x₀，求x₀

22．　　　　　 若x，y满足x²+y²=2x，求x²-y²的最大值和最小值.

21．　　　　　 知f(x)=x+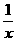，(x≠0)，判断f(x)的奇偶性，并按单调性定义证明，f(x)在(0，1)上是减函数，在(1，+∞)上是增函数.