
题目列表(包括答案和解析)
7、若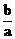 <-1,则方程bx2-ay2=b的曲线是
<-1,则方程bx2-ay2=b的曲线是
A、焦点在x轴上的椭圆 B、焦点在x轴上的双曲线
C、焦点在y轴上的椭圆 D、焦点在y轴上的双曲线翰林汇
6、两条直线mx+y-n=0和x+my+1=0互相平行的条件是
A、m=1
B、m=±1 C、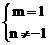 D、
D、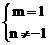 或
或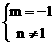
5、直线3x-2y=4 的截距式方程是
A、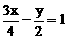 B、
B、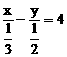 C、
C、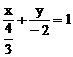 D、
D、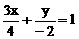
4、直线l: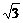 x+y-1=0 的倾斜角是
x+y-1=0 的倾斜角是
A、30º B、60º C、150º D、120º
3、不等式|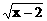 -3|<1的解集是
-3|<1的解集是
A、{ x | 5 < x <16 } B、{x | 6 < x < 18} C、{x | 7 < x <20} D、{x | 8 < x < 22}
2、不等式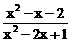 <0的解集是
<0的解集是
A、{x|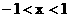 或
或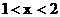 } B、{x|
} B、{x|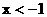 或
或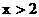 }
}
C、{x | 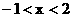 } D、{x|
} D、{x|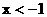 或
或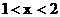 }
}
1、已知a lg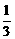 >0,且a+b>0,则有
>0,且a+b>0,则有
A、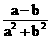 >0 B、
>0 B、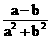 <0 C、
<0 C、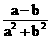 ≥0 D、
≥0 D、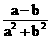 ≤0
≤0
22、双曲线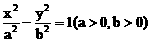 的右支上存在与右焦点和左准线等距离的点,求离心率e的取值范围.
的右支上存在与右焦点和左准线等距离的点,求离心率e的取值范围.
解:设M(x0,y0)是双曲线右支上满足条件的点,且它到右焦点F2的距离等于它到左准线的距离
即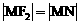 ,由双曲线定义可知
,由双曲线定义可知 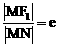 …………………2分
…………………2分
∴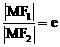 …………………………2分
…………………………2分
推导由焦点半径公式得 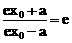 …………………………2分
…………………………2分
∴x0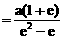 ………………………2分
………………………2分
而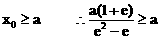 即
即 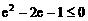 …………………………………2分
…………………………………2分
解得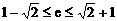 但
但 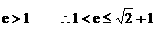 …………………2分
…………………2分
21、已知圆C关于y轴对称,经过抛物线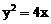 的焦点,且被直线y=x分成两段弧长之比为1:2,求圆C的方程.
的焦点,且被直线y=x分成两段弧长之比为1:2,求圆C的方程.
解:设圆C的方程为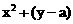
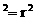 ,抛物线
,抛物线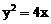 的焦点F(1,0)………………2分
的焦点F(1,0)………………2分
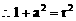 ①
……………………3分
①
……………………3分
又直线y=x分圆的两段弧长之比为1:2,可知圆心到直线y=x的距离等于半径的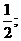
即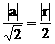 ② …………………3分
② …………………3分
解①、②得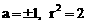 故所求圆的方程为
故所求圆的方程为 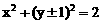 ………4分
………4分
20、(2)班在本届校运会上获团体冠军,学校奖励该班550元,并要求专款专用。经班委会研究决定,将奖金用于购买单价分别为60元、70元的足球和篮球,特别强调:足球至少买3个,篮球至少买2个。由体育委员陈鹏执行,请问陈鹏有多少种不同的购球方式?足球与篮球各买多少个,可以使剩下的钱最少?
解:设购买足球x个,篮球 y个,
依题意得: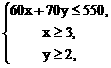 即
即 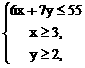 ……………………………………3分
……………………………………3分
画出可行域,找到整点为:(3,2),(3,3),(3,4),(3,5),(4,2),(4,3),(4,4),(5,2),(5,3),(6,2) 在可行域中,
即陈鹏有10种不同的购球方式。 ………………6分
其中点(3,5)使目标函数u= 6x+7y 取最大值umax=53
∴买3个足球、5个篮球,可以使剩下的钱最少。 ………………………3分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com