
题目列表(包括答案和解析)
19.解:设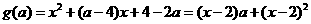 ,
,
则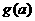 的图象为一直线,在
的图象为一直线,在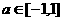 上恒大于0,故有
上恒大于0,故有
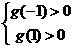 ,即
,即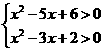 ,解得:
,解得: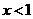 或
或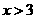
∴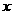 的取值范围是
的取值范围是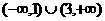
18.证明:法一(综合法)
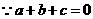 ,
,
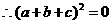
展开并移项得: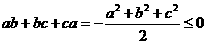
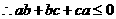
法二(分析法)
要证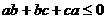 ,
,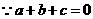 ,故只要证
,故只要证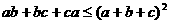
即证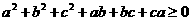 ,
,
也就是证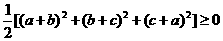 ,
,
而此式显然成立,由于以上相应各步均可逆,∴原不等式成立。
法三: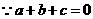 ,
,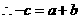
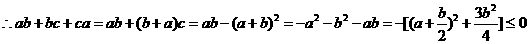
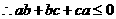
法四: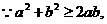
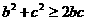 ,
,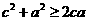
∴由三式相加得: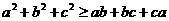
两边同时加上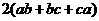 得:
得: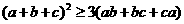
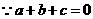 ,
∴
,
∴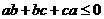
17.解:不等式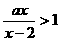 可化为
可化为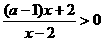 .
.
∵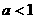 ,∴
,∴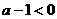 ,则原不等式可化为
,则原不等式可化为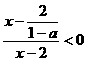 ,
,
故当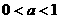 时,原不等式的解集为
时,原不等式的解集为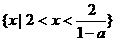 ;
;
当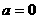 时,原不等式的解集为
时,原不等式的解集为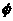 ;
;
当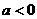 时,原不等式的解集为
时,原不等式的解集为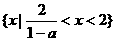 .
.
16.解:原不等式等价于:
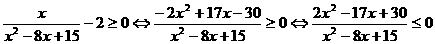
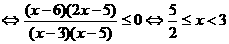 或
或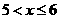
∴原不等式的解集为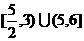
1.C; 2.A; 3.D; 4.C; 5.C; 6.D; 7.A;
8.D; 9.B; 10.A;11. 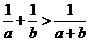 ; 12.
; 12.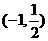 ; 13. 20 ; 14.
; 13. 20 ; 14. 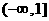 ;15.
;15.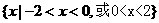 ;
;
21.已知函数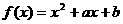 .
.
(1)若对任意的实数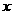 ,都有
,都有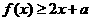 ,求
,求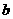 的取值范围;
的取值范围;
(2)当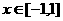 时,
时,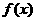 的最大值为M,求证:
的最大值为M,求证: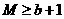 ;
;
(3)若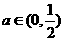 ,求证:对于任意的
,求证:对于任意的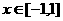 ,
,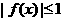 的充要条件是
的充要条件是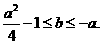
§3.5不等式单元测试
20.如图所示,校园内计划修建一个矩形花坛并在花坛内装置两个相同的喷水器。已知喷水器的喷水区域是半径为5m的圆。问如何设计花坛的尺寸和两个喷水器的位置,才能使花坛的面积最大且能全部喷到水?
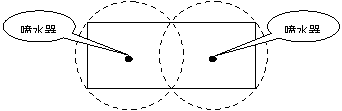
19.对任意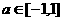 ,函数
,函数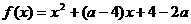 的值恒大于零,求
的值恒大于零,求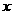 的取值范围。
的取值范围。
18.已知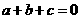 ,求证:
,求证: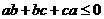 。
。
17.已知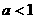 ,解关于
,解关于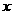 的不等式
的不等式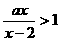 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com