
题目列表(包括答案和解析)
19.(本小题满分12分)省工商局于2007年3月份,对全省流通领域的饮料进行了质量监督抽查,结果显示,某种刚进入市场的x饮料的合格率为80%,现有甲,乙,丙3人聚会,选用6瓶x饮料,并限定每人喝2瓶,求:
(1)甲喝2瓶合格的x饮料的概率;
(2)甲,乙,丙3人中只有1人喝2瓶不合格的x饮料的概率(精确到0.01).
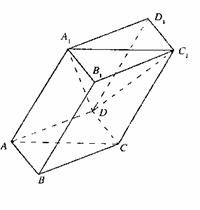 20.(本小题满分13分)如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,
20.(本小题满分13分)如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,
∠ABC=60°,平面AA1C1C⊥平面ABCD,∠A1AC=60°.
(1)证明:BD⊥AA1;
(2)求二面角D-A1A-C的平面角的余弦值;
(3)在直线CC1上是否存在点P,使BP//平面DA1C1?
若存在,求出点P的位置;若不存在,说明理由.
18. (本小题满分12分)已知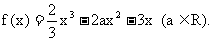
(1)当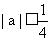 时, 求证:
时, 求证: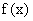 在
在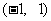 内是减函数;
内是减函数;
(2)若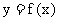 在
在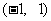 内有且只有一个极值点, 求a的取值范围
内有且只有一个极值点, 求a的取值范围
17.(本小题满分12分)已知10件产品中有3件是次品.
(1)任意取出3件产品作检验,求其中至少有1件是次品的概率;
(2)为了保证使3件次品全部检验出的概率超过0.6,最少应抽取几件产品作检验?
16、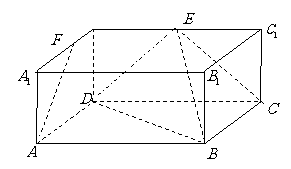 (12分)如图,在长方体
(12分)如图,在长方体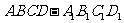 中,
中,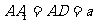 ,
,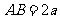 ,
,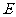 、
、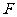 分别为
分别为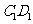 、
、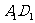 的中点.
的中点.
(1)求证: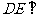 平面
平面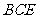 ;
;
(2)求证: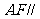 平面
平面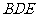 .
.
15. (1-x)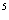 (1+x+x
(1+x+x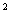 )
)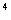 的展开式中x
的展开式中x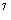 项的系数是__________,
项的系数是__________,
各项系数和为__________
14.某公司一年购买某种货物400吨,每次都购买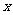 吨,运费为4万元/次,一年的总存储费用为
吨,运费为4万元/次,一年的总存储费用为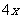 万元,要使一年的总运费与总存储费用之和最小,则
万元,要使一年的总运费与总存储费用之和最小,则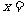
吨.
13. 某种产品有3只次品和6只正品,每次取出一只测试,直到3只次品全部测出为止,求第三只次品在第6次测试时被发现的不同的测试情况有_________种.
12.已知曲线C: ,直线
,直线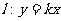 ,且直线
,且直线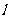 与曲线C相切于点
与曲线C相切于点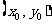
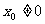 ,则直线
,则直线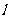 的方程____________ ,切点坐标__________ ..
的方程____________ ,切点坐标__________ ..
11. 若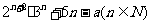 能被25整除,则a的最小正数值是___________ .
能被25整除,则a的最小正数值是___________ .
10. 设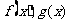 在[m,n]上可导, 且
在[m,n]上可导, 且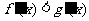 , 则当
, 则当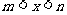 时,有 ( )
时,有 ( )
A. 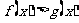 .
B.
.
B.
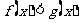
C. 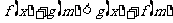 .
D.
.
D. 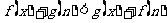
Ⅱ卷(满分100分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com