
题目列表(包括答案和解析)
5、已知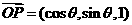 ,
,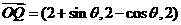 ,
,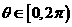 ,则当
,则当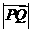 最大时
最大时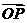 与
与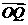 的夹角
的夹角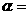
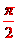 。
。
解: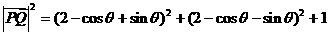
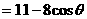 ,当
,当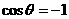 时,
时,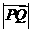 最大。
最大。
此时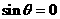 ,代入得
,代入得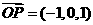 ,
,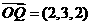 。
。
 因为
因为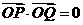 ,所以
,所以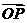 与
与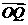 的夹角
的夹角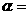
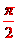 。
。
4、在等比数列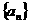 中,公比为
中,公比为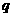 且
且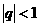 ,若
,若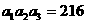 ,
,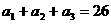 ,则
,则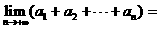
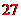 。
。
解: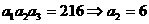 ,
,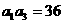 ,
,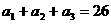
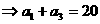 。
。
因为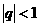 ,解得
,解得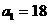 ,
,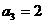 ,所以
,所以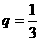 。
。
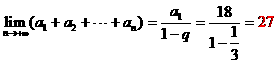 。
。
3、设正三棱椎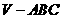 的底边长为
的底边长为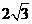 ,高为
,高为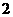 ,则侧棱与底面所成角的大小为
,则侧棱与底面所成角的大小为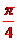 。
。
2、若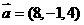 ,
,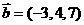 ,则
,则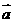 与
与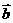 的位置关系为
的位置关系为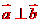 。
。
1、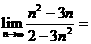
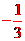 。
。
20.(本小题满分16分)
设z是虚数,ω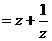 是实数,且-1<ω<2.
是实数,且-1<ω<2.
(1)求 |z| 的值及z的实部的取值范围;
(2)设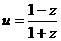 ,求证:u为纯虚数;
,求证:u为纯虚数;
(3)求ω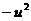 的最小值.
的最小值.
高二数学下第二次半月考试卷
19.(本小题满分16分)
已知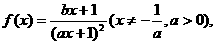 且
且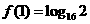 ,
,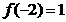 .
.
(1)求函数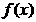 的表达式;
的表达式;
(2)已知数列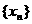 的项满足
的项满足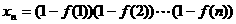 ,试求
,试求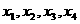 ;
;
(3)猜想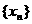 的通项,并用数学归纳法证明.
的通项,并用数学归纳法证明.
18.(本小题满分16分)
若某一等差数列的首项为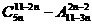 ,公差为
,公差为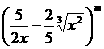 展开式中的常数项,其中m是7777-15除以19的余数,则此数列前多少项的和最大?并求出这个最大值。
展开式中的常数项,其中m是7777-15除以19的余数,则此数列前多少项的和最大?并求出这个最大值。
17.(本小题满分14分)
甲、乙两名射击运动员,甲射击一次命中10环的概率为0.5,乙射击一次命中10环的概率为s,若他们独立的射击两次,设乙命中10环的次数为X,则E(X)=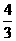 ,Y为甲与乙命中10环的次数差的绝对值. 求s的值及Y的分布列及数学期望.
,Y为甲与乙命中10环的次数差的绝对值. 求s的值及Y的分布列及数学期望.
16.(本小题满分14分)
(1)设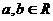 ,若矩阵
,若矩阵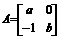 把直线
把直线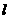 :
: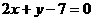 变换为另一直线
变换为另一直线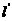 :
: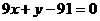 ,求
,求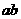 的值.
的值.
(2)已知直线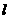 经过点
经过点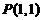 ,倾斜角
,倾斜角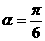 ,
,
(I)写出直线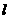 的参数方程
的参数方程
(II)设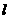 与圆
与圆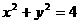 相交与两点
相交与两点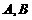 ,求点
,求点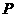 到
到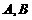 两点的距离之积
两点的距离之积
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com