
题目列表(包括答案和解析)
6、曲线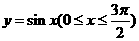 与坐标轴围成的面积是( )
与坐标轴围成的面积是( )
A.4 B. 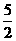 C.3
D.2
C.3
D.2
5、过点(-1,0)作抛物线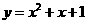 的切线,则其中一条切线为( )
的切线,则其中一条切线为( )
A. 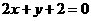 B.
B. 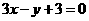
C. 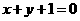 D.
D. 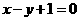
4、已知某物体的运动方程是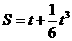 , 则当
, 则当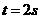 时的瞬时速度是 ( )
时的瞬时速度是 ( )
A. 10m /s B. 9m /s C. 4m /s D. 3m /s
3、复数 =3+i,
=3+i,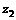 =1-i,则
=1-i,则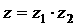 在复平面内对应的点位于( )
在复平面内对应的点位于( )
A第一象限内 B第二象限内 C第三象限内 D第四象限内
2、曲线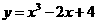 在点
在点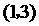 处的切线的倾斜角为( )
处的切线的倾斜角为( )
A.30° B.45° C.60° D.120°
1、函数y=(2x+1)3在x=0处的导数是( )
A.0 B.1 C.3 D.6
(17).(本题满分10分)已知函数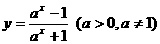
(Ⅰ)求函数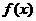 的定义域,值域;(Ⅱ)讨论函数
的定义域,值域;(Ⅱ)讨论函数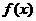 的单调性
的单调性
(18)、(本题满分12分)已知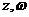 为复数,
为复数,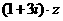 为纯虚数,
为纯虚数,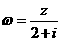 ,且
,且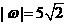 。求复数
。求复数 。
。
(19). (本题满分12分)已知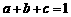 ,求证:
,求证: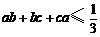
(20). (本题满分12分)已知集合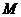 是满足下列性质的函数
是满足下列性质的函数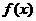 的全体:在定义域内存在
的全体:在定义域内存在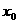 ,使得
,使得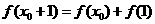 成立.
成立.
(Ⅰ)函数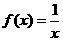 是否属于集合
是否属于集合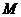 ?说明理由;
?说明理由;
(Ⅱ)设函数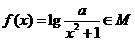 ,求
,求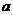 的取值范围;
的取值范围;
(21). (本题满分12分)已知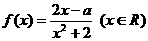 在区间[-1,1]上是增函数.
在区间[-1,1]上是增函数.
(Ⅰ)求实数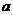 的值组成的集合
的值组成的集合 ;
;
(Ⅱ) 设关于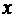 的方程f(
的方程f(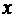 )=
)=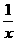 的两个非零实根为
的两个非零实根为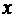 1、
1、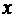 2.试问:是否存在实数m,使得不等式m2+tm+1≥|
2.试问:是否存在实数m,使得不等式m2+tm+1≥|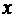 1-
1-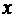 2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
(22).(本小题满分12分)已知函数错误!嵌入对象无效。的定义域是错误!嵌入对象无效。∈R,错误!嵌入对象无效。Z},且错误!嵌入对象无效。,错误!嵌入对象无效。,当错误!嵌入对象无效。时,错误!嵌入对象无效。.
(Ⅰ)求证:错误!嵌入对象无效。是奇函数;
(Ⅱ)求错误!嵌入对象无效。在区间错误!嵌入对象无效。Z)上的解析式;
(Ⅲ)是否存在正整数k,使得当x∈错误!嵌入对象无效。时,不等式错误!嵌入对象无效。有解?证明你的结论.
沈阳二中2008--2009学年度下学期3月月考
(13).函数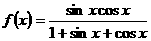 的值域是____
的值域是____

(15).函数f(x)=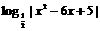 的单调递增区间为 .
的单调递增区间为 .
(16).在计算机的算法语言中有一种函数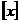 叫做取整函数(也叫高斯函数)。它表示不超过x的最大整数。如
叫做取整函数(也叫高斯函数)。它表示不超过x的最大整数。如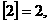
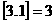 ,
,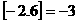 .设函数
.设函数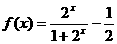 ,则函数
,则函数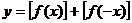 取值的集合为
取值的集合为
(1).若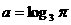 ,
, 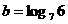 ,
,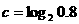 , 则( )
, 则( )
A . 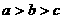 B.
B. 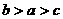 C.
C. 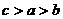 D.
D. 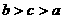
(2).已知函数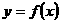 ,
,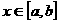 ,那么集合
,那么集合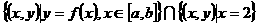 中元素的个数为( )
中元素的个数为( )
A. 1 B. 0 C. 1或0 D. 1或2
(3).已知函数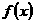 的定义域为[0,1],值域为[1,2],则函数
的定义域为[0,1],值域为[1,2],则函数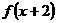 的定义域和值域分别是( )
的定义域和值域分别是( )
A. [2,3] , [1,2] B. [2,3] , [3,4]
C. [-2,-1] ,[1,2] D. [-1,2] , [3,4]
(4). 已知0<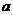 <1,
<1,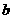 <-1,则函数
<-1,则函数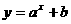 的图象必定不经过( )
的图象必定不经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
(5).给出以下命题:
①合情推理是由特殊到一般的推理,得到的结论不一定正确,演绎推理是由一般到特殊的推理,得到的结论一定正确;
②甲乙两名同学各自独立考察两个变量X,Y的线性关系时,发现两人对X的观察数据的平均值相等,都是s, 对Y的观察数据的平均值也相等,都是t,各自求出的回归方程分别是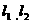 ,则直线
,则直线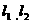 必定相交于点(s,t);
必定相交于点(s,t);
③函数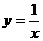 (
(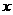 >-4)的值域是
>-4)的值域是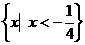
④用独立性检验(2 2列联表)来考察两个变量X 与Y是否有关系时,算出的随机变量
2列联表)来考察两个变量X 与Y是否有关系时,算出的随机变量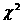 值越大,说明“X 与Y有关系”成立的可能性越大。
值越大,说明“X 与Y有关系”成立的可能性越大。
其中真命题的序号是( )
A. ①②③ B. ①③④ C. ②④ D. ①③
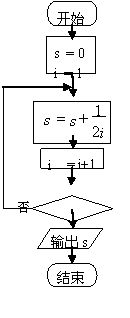 (6).已知回归直线的斜率的估计值是 1.23,样本点的中心为(4,5),则回归直线的方程是( ).
(6).已知回归直线的斜率的估计值是 1.23,样本点的中心为(4,5),则回归直线的方程是( ).
A.y=1.23x+4 B.y=1.23x+5 C.y=1.23x+0.08 D.y=0.08x+1.23
(7)..若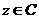 且
且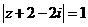 ,则
,则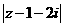 的最小值是:( )
的最小值是:( )
A 2 B 3 C 4 D 5
(8).给出的是计算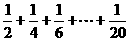 的值的一个流程图,其中判框内应填入的条件是( )
的值的一个流程图,其中判框内应填入的条件是( )
 (A)
(A) 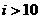 (B)
(B) 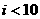 (C)
(C) 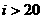 (D)
(D) 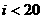
(9). 在养分充足的情况下,细菌的数量会以指数函数的方式成长,假设细菌A的数量每2小时可以为原来的2倍;细菌B的数量每5小时可以为原来的4倍。现在若养分充足且一开始两种细菌的数量相等,则经过( )小时后,细菌A的数量是细菌B的数量的2倍。
A.5 B.10 C.15 D.30
(10).已知错误!嵌入对象无效。是定义在错误!嵌入对象无效。上的偶函数,且在错误!嵌入对象无效。上单调递增,则不等式错误!嵌入对象无效。的解集是( )
A.错误!嵌入对象无效。 B.错误!嵌入对象无效。 C.错误!嵌入对象无效。∪错误!嵌入对象无效。 D.不能确定
(11).二次函数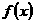 满足
满足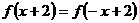 ,又
,又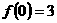 ,
,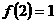 ,若在[0,
,若在[0, ]上有最大值3,最小值1,则
]上有最大值3,最小值1,则 的取值范围是( )
的取值范围是( )
A. 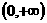 B.
B. 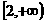 C.
C.
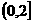 D.
[2,4]
D.
[2,4]
(12).已知定义域是R的函数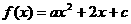 的值域是
的值域是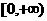 ,那么
,那么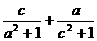 的最小值是( )
的最小值是( )
A.1 B.2 C.3 D.4
第II卷 (共90分)
命题人 黄岩 审校人 陈玉成
第Ⅰ卷(选择题 共60分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com