
5.若双曲线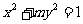 的离心率是2,则实数
的离心率是2,则实数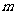 的值是 ( )
的值是 ( )
A. B.
B.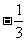 C.3 D.
C.3 D.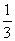
4.等差数列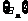 中,
中,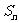 是前n项和,且
是前n项和,且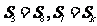 ,则
,则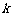 的值为 ( )
的值为 ( )
A.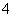 B
B
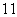 C.
C.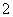 D
D
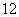
3.已知向量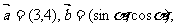 且
且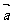 ⊥
⊥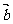 ,则
,则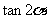 = ( )
= ( )
A.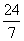 B.
B.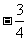 C.
C.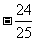 D.
D.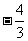
2.(理)已知i是虚数单位,复数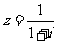 在复平面内对应的点在 ( )
在复平面内对应的点在 ( )
A.第一象限 B.第三象限 C.第二象限 D.第四象限
(文) 函数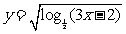 的定义域是 ( )
的定义域是 ( )
A.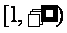 B.
B.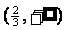 C.
C.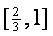 D.
D.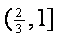
1.已知集合A=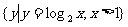 ,B=
,B=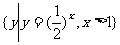 ,则A∩B等于
( )
,则A∩B等于
( )
A.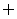 B.
B.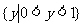 C.
C.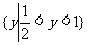 D.
D.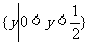
20.(本小题共14分)
已知函数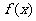 定义域为R,满足:
定义域为R,满足:
①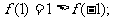
②对任意实数x,y有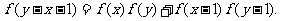
(1)求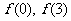 的值;
的值;
(2)求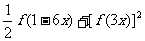 的值;
的值;
(3)是否存在常数A,B,使得不等式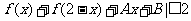 对一切实数x均成立。如果存在,求出常数A,B的值;如果不存在,请说明理由。
对一切实数x均成立。如果存在,求出常数A,B的值;如果不存在,请说明理由。
19.(本小题共13分)
已知抛物线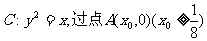 作直线l交抛物线于P、Q(点P在第一象限)。
作直线l交抛物线于P、Q(点P在第一象限)。
(1)当点A是抛物线C的焦点,且弦长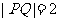 时,求直线l的方程;
时,求直线l的方程;
(2)设点Q关于x轴的对称点为M,直线PM交x轴于点B,且BP⊥BQ。求证B的坐标是(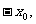 0)并求点B到直线l的距离d的取值范围。
0)并求点B到直线l的距离d的取值范围。
18.(本小题共13分)
已知函数
(1)求函数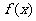 的定义域及单调区间;
的定义域及单调区间;
(2)若存在实数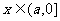 ,使得不等式
,使得不等式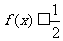 成立,求a的取值范围。
成立,求a的取值范围。
17.(本小题共14分)
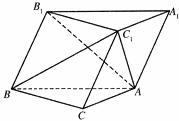
如图,斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,点B1在底面ABC内的射影恰好是BC的中点,且BC=CA=AA1。
(1)求证:平面ACC1A1⊥平面B1C1CB;
(2)求证:BC1⊥AB;
(3)求二面角B-AB1-C1的大小。
16.(本小题共13分)
检测部门决定对某市学校教室的空气质量进行检测,空气质量分别为A、B、C三级。每间教室的检测方式如下:分别在同一天的上、下午各进行一次检测,若两次检测中有C级或两次都是B级,则该教室空气质量不合格,设各教室的空气质量相互独立,且每次检测的结果也相互独立,根据多次抽检结果,一间教室一次检测空气质量为A、B、C三级的频率依次为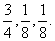
(1)在该市的教室中任取一间,估计该间教室空气质量合格的概率;
(2)如果对该市某中学的4间教室进行检测,记在上午检测空气质量为A级的教室间数为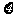 ,并以空气质量为A级的频率作为空气质量为A级的概率,求
,并以空气质量为A级的频率作为空气质量为A级的概率,求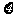 的分布列及期望。
的分布列及期望。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com