
6.某校高三年级共有六个班级,现从外地转入4名学生,要安排到该年级的两个班级且每班安排2名,则不同的安排方案种数为 ( )
A.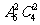 B.
B.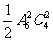 C.
C.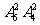 D.
D.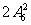
5.已知m、n是不重合的直线,α、β是不重合的平面,有下列命题:
①若m α,n∥α,则m∥n;
α,n∥α,则m∥n;
②若m∥α,m∥β,则α∥β;
③若α∩β=n,m∥n,则m∥α且m∥β;
④若m⊥α,m⊥β,则α∥β.
其中真命题的个数是 ( )
A.0 B.1 C.2 D.3
4.已知F1、F2是椭圆的两个焦点,过F1且与椭圆长轴垂直的直线交椭圆于A、B两点,若△ABF2是正三角形,则这个椭圆的离心率是 ( )
A.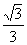 B.
B.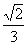 C.
C.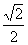 D.
D.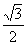
3.命题p:若a、b∈R,则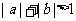 是
是 的充分而不必要条件;
的充分而不必要条件;
命题q:函数y=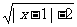 的定义域是(-∞,-1
的定义域是(-∞,-1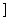 ∪[3,+∞
∪[3,+∞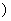 。则 ( )
。则 ( )
A.“p或q”为假 B.“p且q”为真 C.p真q假 D.p假q真
2.tan15°+cot15°的值是 ( )
A.2 B.2+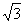 C.4 D.
C.4 D.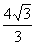
1.复数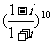 的值是 ( )
的值是 ( )
A.-1 B.1 C.-32 D.32
22.(本题满分12分)
已知函数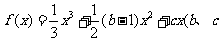 为常数)
为常数)
(1)若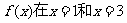 处取得极值,求b,c的值;
处取得极值,求b,c的值;
(2)若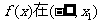 和
和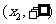 内单调递增,在
内单调递增,在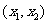 内单调递减,且满足
内单调递减,且满足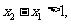 求证:
求证: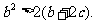
21.(本题满分12分)
在直角坐标平面内,已知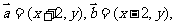 且
且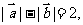
(1)求点M(x,y)的轨迹C的方程;
(2)过点P(2,0)作倾斜角为锐角的直线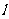 与曲线C交于A、B两点,且
与曲线C交于A、B两点,且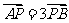 ,求直线
,求直线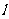 的方程。
的方程。
20.(本题满分12分)
若数列{an}满足前n项和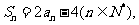
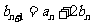 且
且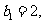 求
求
(1){bn}的通项公式;
(2){bn}的前n项和Tn。
19.(本题满分12分)
如图,在正四棱柱ABCD-A1B1C1D1中,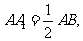 点E、M分别为A1B、C1C的中点,过A1、B、M三点的平面A1BMN交C1D1于点N。
点E、M分别为A1B、C1C的中点,过A1、B、M三点的平面A1BMN交C1D1于点N。
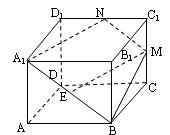
(1)求证:EM//平面A1B1C1D1;
(2)求二面角B-A1N-B1的正切值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com