
3.某小组共有8名同学,其中男生6人,女生2人,现从中按性别分层随机抽4人参加一项公益活动,则不同的抽取方法有 ( )
A.40种 B.70种 C.80种 D.240种
2.已知ab=1,函数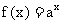 与函数
与函数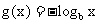 的图象可能是 ( )
的图象可能是 ( )
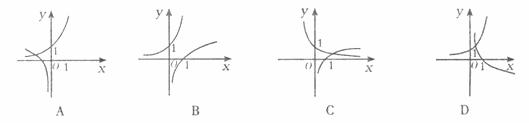
1.设集合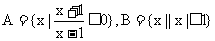 ,那么“
,那么“ 是
是 ”的 ( )
”的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
22.(本题14分)下图的一组图形为某一四棱锥S-ABCD的侧面与底面。
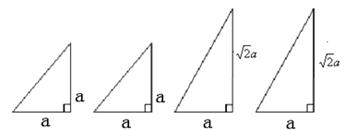
(1)请画出四棱锥S-ABCD的示意图,是否存在一条侧棱垂直于底面?如果存在,请给出证明;如果不存在,请说明理由;
(2)若SA⊥面ABCD,E为AB中点,求二面角E-SC-D的大小;
(3)求点D到面SEC的距离。
21.(本题12分)已知双曲线C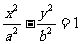 (a>0,b>0)的两个焦点为F1(-2,0),F2(2,0),点P(3,
(a>0,b>0)的两个焦点为F1(-2,0),F2(2,0),点P(3,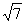 )的曲线C上。
)的曲线C上。
(Ⅰ)求双曲线C的方程;
(Ⅱ)记O为坐标原点,过点Q(0,2)的直线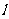 与双曲线相交于不同的两点E、F,若△OEF的面积为
与双曲线相交于不同的两点E、F,若△OEF的面积为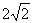 ,求直线
,求直线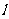 的方程。
的方程。
20.(本小题满分12分)已知直三棱柱ABC-A1B1C1中,B1C1=A1C1,AC1⊥A1B。M,N分别为A1B1,AB的中点。
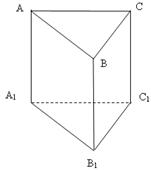
(1)求证:平面AMC1∥平面NB1C;
(2)求A1B与B1C所成的角的大小;
(3)若A1C1=AA1=1,∠A1C1B1=90°,求三棱锥B-B1CN的体积。
19.由-1,0,1,2,3这5个数中选3个不同的数作为二次函数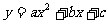 的系数。
的系数。
(1)开口向上且不过原点的抛物线有几条?
(2)与 轴的负半轴至少有一个交点的抛物线有多少条?
轴的负半轴至少有一个交点的抛物线有多少条?
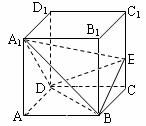
18.(本题12分)已知正方体ABCD-A1B1C1D1中,E为棱CC1上的动点。
(Ⅰ)求证:A1E⊥BD;
(Ⅱ)若平面A1BD⊥平面EBD,试确定E点的位置。
17.(本题12分)已知甲组有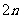 人,乙组有
人,乙组有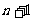 人,设从甲组中选出3人分别参加数、理、化三科竞赛(每科竞赛限一人参加)的选法数是
人,设从甲组中选出3人分别参加数、理、化三科竞赛(每科竞赛限一人参加)的选法数是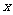 ,从乙组中选出4人站成一排照相的站法数是
,从乙组中选出4人站成一排照相的站法数是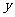 ,若
,若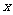 =2
=2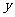 ,求
,求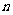 、
、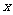 和
和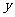 。
。
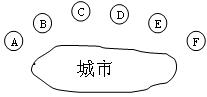
16.某市为改善生态环境,计划对城市外围A、B、C、D、E、F六个区域(如图)进行治理,第一期工程拟从这六个区域中选取三个,根据要求至多有两个区域相邻,则不同的选取方案共有 种(用数字作答)。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com