
4.已知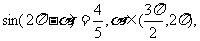 则
则 等于 ( )
等于 ( )
A.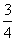 B.
B. C.
C.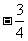 D.
D.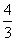
3.下列函数中既是奇函数,又在区间(0,1)上单调递减的是 ( )
A.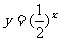 B.
B.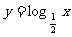 C.
C.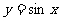 D.
D.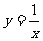
2.不定式 的解集为 ( )
的解集为 ( )
A. B.
B.
C. D.
D.
1.设集合U={1,2,3,4,5},A={1,2,3},B={2,3,4}则CU(A∩B)= ( )
A.{2,3} B.{1,4,5} C.{4,5} D.{1,5}
22.(本题满分12分)
在△ABC中,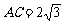 ,B是椭圆
,B是椭圆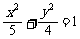 的上顶点,l是双曲线
的上顶点,l是双曲线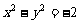 位于x轴下方的准线,当AC在直线l上运动时.
位于x轴下方的准线,当AC在直线l上运动时.
(1)求△ABC外接圆的圆心P的轨迹E的方程;
(2)过定点F(0,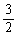 )作互相垂直的直线l1、l2,分别交轨迹E于M、N和R、Q;求四边形MRNQ的面积的最小值;
)作互相垂直的直线l1、l2,分别交轨迹E于M、N和R、Q;求四边形MRNQ的面积的最小值;
21.(本题满分12分)
已知数列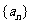 中,
中,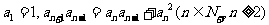 ,且
,且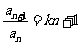 ;
;
(1)求证: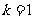 ;
;
(2)设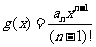 ,
,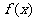 是数列
是数列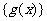 的前
的前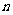 项和,求
项和,求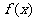 的解析式;
的解析式;
(3)求证:不等式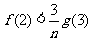 对于
对于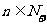 恒成立;((3)问只理科生做,文科生不做)
恒成立;((3)问只理科生做,文科生不做)
20.(本题满分12分)
已知函数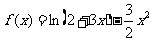 ;
;
(1)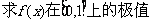 ;
;
(2)若对于任意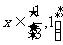 ,不等式
,不等式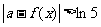 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(3)若关于x的方程 在
在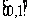 上恰有两个不同的实根,求实数b的取值范围;
上恰有两个不同的实根,求实数b的取值范围;
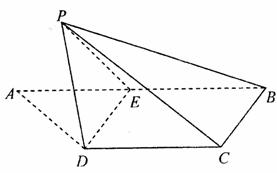
19.如图,梯形ABCD中,CD//AB,AD=DC=CB=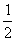 AB=1,E是AB的中点,将△ADE沿DE折起,使点A折到点P的位置,且二面角P-DE-C的大小为120°。
AB=1,E是AB的中点,将△ADE沿DE折起,使点A折到点P的位置,且二面角P-DE-C的大小为120°。
(1)求证:DE⊥PC;
(2)求直线PD与平面BCDE所成角的大小;
(3)求点D到平面PBC的距离。
18.(本题满分12分)
一袋中装有分别标记着1、2、3、4数字的4个球, 从这只袋中每次取出1个球,取出后放回, 连续取三次, 设三次取出的球中数字最大的数为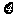 ;
;
(1)求 时的概率;
时的概率;
(2)求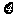 的概率分布列及数学期望;
的概率分布列及数学期望;
17.(本题满分10分)
在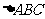 中,角
中,角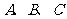 的对边分别为
的对边分别为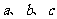 ,
,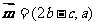 ,
,
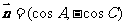 ,且
,且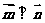 ;
;
(1)求角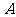 的大小;
的大小;
(2)当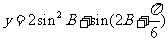 取最大值时,求角
取最大值时,求角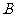 的大小;
的大小;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com