3．以原点为顶点，x轴为对称轴且焦点在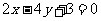上的抛物线方程是　　　　 。

2．设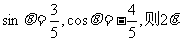的终边所在的象限是　　　　　 。

1．不等式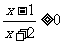的解集为　　　　　　 。

21．(本题满分18分，第1小题满分4分，第2小题满分6分，第3小题满分8分)

　　　　 冬天，洁白的雪花飘落时十分漂亮。为研究雪花的形状，1904年，瑞典数学家科克(Koch Heige Von)把雪花理想化，得到了雪花曲线，也叫科克曲线。它的形成过程如下：

　 (i)将正三角形(图①)的每边三等分，并以中间的那一条线段为一底边向形外作等边三角形，然后去掉底边，得到图②；

　 (ii)将图②的每边三等分，重复上述作图方法，得到图③；

　 (iii)再按上述方法无限多次继续作下去，所得到的曲线就是雪花曲线。

　　　　 将图①、图②、图③……中的图形依次记作M₁、M₂、…、M_n…设M₁的边长为1。

　　 求：(1)M_n的边数；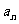

　　　 (3)M_n的面积S_n的极限。

20．(本题满分16分，第1小题满分6分，第2小题满分10分)

设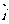、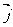为直角坐标平面内x、y轴正方向上的单位向量，若向量，

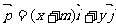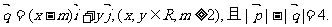
　 (1)求动点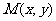的轨迹方程？并指出方程所表示的曲线；

　 (2)已知点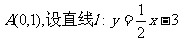与点M的轨迹交于B、C两点，问是否存在实数m，使得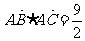？若存在，求出m的值；若不存在，说明理由。

19．(本题满分14分)

　　　　 设m、n为正整数，且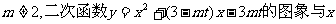轴的两个交点间的距离为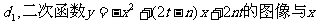轴的两个交点间的距离为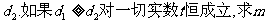、n的值。

18．(本题满分14分)

　　　　 在△ABC中，角A，B，C所对边分别为a，b，c，已知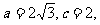

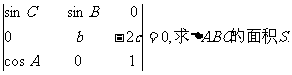
17．(本题满分12分)

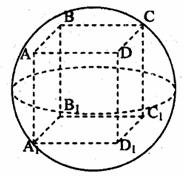
　　 已知各顶点都在一个球面上的正四棱柱高为4，体积为16，求这个球的表面积。

16．对于直角坐标平面内的任意两点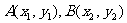，定义它们之间的一种“距离”：

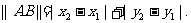　　 给出下列三个命题：

　　　 ①若点C在线段AB上，则；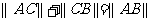

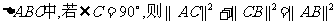　　　 ③在。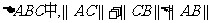

　　 其中真命题的个数为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．0　　　　　　　　　　　　 B．1　　　　　　　　　　　　 C．2　　　　　　　　　　　　 D．3

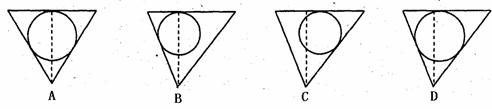
15．在一个倒置的正三棱锥容器中，放入一个钢球，钢球恰好与棱锥的四个面都接触，经过棱锥的一条侧棱和高作截面，正确的截面图为　　　　　　　　　　　　　　　　　　　 (　　 )