
4.若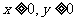 ,且
,且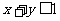 ,则
,则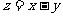 的最大值是
的最大值是
A.1 B.2 C.-1 D.-2
3.已知函数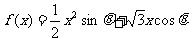 ,其中
,其中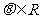 ,则
,则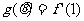 的取值范围是
的取值范围是
A.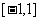 B.
B.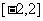 C.
C.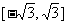 D.
D.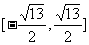
2.“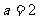 ”是“直线
”是“直线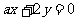 平行于直线
平行于直线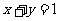 ”的
”的
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
1.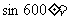
A.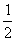 B.
B.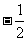 C.
C.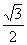 D.
D.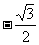
21.(本题满分13分)设数列{an},{bn}满足a1 =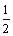 ,2nan+ 1 = (n
+ 1)an,且bn = ln(1 + an)
+
,2nan+ 1 = (n
+ 1)an,且bn = ln(1 + an)
+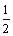
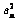 ,n∈N*.
,n∈N*.
(1)求数列{an}的通项公式;(2)对一切n∈N*,证明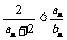 成立;
成立;
(3)记数列{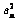 },{bn}的前n项和分别为An,Bn,证明2Bn – An<4.
},{bn}的前n项和分别为An,Bn,证明2Bn – An<4.
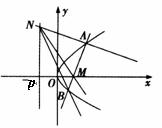
20.(本题满分13分)如图,过定点M(p,0) (p>0)的直线l与抛物线y2 = 2px (p>0)相交于A、B两点.
(1)证明:A、B两点的纵坐标之积为定值;(2)若点N是定直线x = –p上的任一点,问三条直线AN、MN、BN的斜率之间是否存在某等量关系,若存在,试写出该等量关系式,并给出证明;若不存在,说明理由。
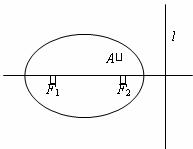
19.(本题满分13分)边界为椭圆形的某运动场(如图所示),椭圆的左右焦点分别为F1,F2,椭圆上的点到焦点F2的最小距离为10米,椭圆的离心率为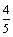 ,①求椭圆的标准方程;②在运动场的右侧,有一条与F1F2垂直的目标线l,它与F2的距离为22.5米,运动员体能训练时,要求从F2的正北方10米处一定点A出发,在椭圆的内外折返快速奔跑,在椭圆的内部是草坪(软地)外部是塑胶跑道。已知某运动员在椭圆内、外奔跑速度之比为4: 5,在草坪的奔跑速度为7m/s,现要求从点A出发,沿任何方向到达目标线l上,求所需的最短时间t.
,①求椭圆的标准方程;②在运动场的右侧,有一条与F1F2垂直的目标线l,它与F2的距离为22.5米,运动员体能训练时,要求从F2的正北方10米处一定点A出发,在椭圆的内外折返快速奔跑,在椭圆的内部是草坪(软地)外部是塑胶跑道。已知某运动员在椭圆内、外奔跑速度之比为4: 5,在草坪的奔跑速度为7m/s,现要求从点A出发,沿任何方向到达目标线l上,求所需的最短时间t.
18.(本题满分12分)将圆x2 + y2 + 2x – 2y = 0按向量a = (1,–1)平移得到圆O,直线l和圆O相交于A、B两点,若在圆O上存在点C,使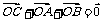 ,且
,且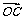 =
=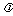 a.
a.
(1)求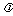 的值;(2)求弦AB的长;(3)求直线l的方程.
的值;(2)求弦AB的长;(3)求直线l的方程.
17.(本题满分12分)定义在R上的单调函数f (x)满足f (3) = log23且对任意x,y∈R都有f (x + y) = f (x) + f (y).
(1)求证f (x)为奇函数;
(2)若f (k·3x) + f (3x – 9x –2)<0对任意x∈R恒成立,求实数k的取值范围.
16.(本题满分12分)向量a = (cosx
+ sinx,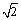 cosx),b = (cosx
– sinx,
cosx),b = (cosx
– sinx,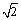 sinx),f (x) = a·b.
sinx),f (x) = a·b.
(1)求函数f (x)的单调区间;
(2)若2x2 – x≤0,求函数f (x)的值域.
x≤0,求函数f (x)的值域.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com