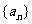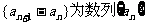22．(本小题满分14分)对于数列，定义数列的“差数列”。若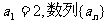的“差数列”的通项为。

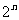　 (1)求数列{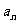}的前n项和；

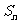　 (2)对(1)中的数列{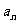}，若数列{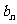}满足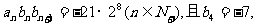

①求数列{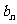}的通项公式；

②数列{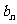}的前n项的积最大时求n的值。

21．(本小题满分14分)设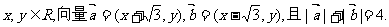

　 (1)求点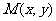的轨迹C的方程；

　 (2)过点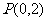的直线l交曲线C于A，B两点(A在P，B之间)，设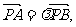直线l的斜率为k，当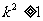时，求实数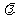的取值范围。

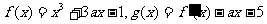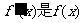20．(本小题满分12分)已知函数，其中的导函数。

　 (1)对满足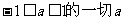的值，都有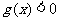，求实数x的取值范围；

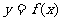　 (2)设，当实数m在什么范围内变化时，使函数的图象与直线y=3只有一个公共点。

19．(本小题满分12分)直三棱柱ABC-A₁B₁C₁的底面ABC为等腰三角形，∠ACB=90°AC=1。C点到AB₁的距离为CE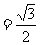，D到AB的中点。

　 (1)求证：AB₁⊥平面CED；

　 (2)求二面角B­­₁-AC-B的平面角的正切值。

18．(本小题满分12分)甲、乙两从进行棋类比赛，在每一局比赛中，甲获胜的概率为P。

　 (1)如果甲，乙两人共比赛4局，甲恰好负2局的概率不大于其恰好胜3局的概率，试求p 的取值范围。

　 (2)若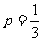，此规则为胜1 局得1分，负1局得0分，共比了3 局，记录的得分为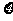，求值变量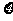的分布列和数学期望 。

17．(本小题满分12分)设函数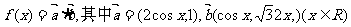

　 (1)若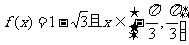，求x；

　 (2)若函数平移后得到函数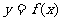的图像，求实数m, n的值。

16．[x]表示不超过x的最大整数，对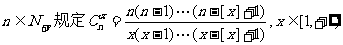

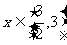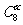则时，的值域为　　　　　　 .

15．正方体ABCD-A₁B₁C₁D₁的棱长是1，侧面BCC₁B₁上到点A的距离为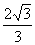的点的集合形成一条曲线，那么这条曲线的长度是　　 　　　　.

14．函数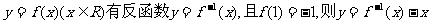的图象过点　　　　　　 .

13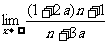．=5，则a=　　　　　　 .