
19.(14分)已知数列{an}的前n项和的公式是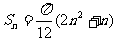 .
.
(1)求证:{an}是等差数列,并求出它的首项和公差;
(2)记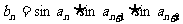 ,求出数列{
,求出数列{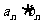 }的前n项和Tn。
}的前n项和Tn。
18.(14分)已知函数f(x)=ax3+3x2-x+1,问是否存在实数a,使得f(x)在(0,4)上单调递减?若存在,求出a的范围;若不存在,说明理由。
17.(14分)某工厂生产甲、乙两种产品,已知生产每吨甲、乙两种产品所需煤、电力、劳动力、获得利润及每天资源限额(最大供应量)如下表所示:
|
甲产品 (每吨) |
乙产品 (每吨) |
资源限额 (每天) |
|
煤(t) |
9 |
4 |
360 |
|
电力(kw·h) |
4 |
5 |
200 |
|
劳力(个) |
3 |
10 |
300 |
|
利润(万元) |
6 |
12 |
|
问:每天生产甲、乙两种产品各多少吨,获得利润总额最大?
16.(12分) 在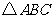 中,内角
中,内角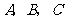 对边的边长分别是
对边的边长分别是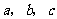 ,已知
,已知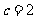 ,
,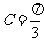 .
.
(Ⅰ)若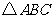 的面积等于
的面积等于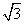 ,求
,求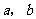 ;
;
(Ⅱ)若 ,求
,求 的面积.
的面积.
15.(12分)已知函数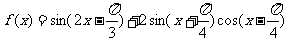
(Ⅰ)求函数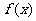 的最小正周期和图象的对称轴方程;
的最小正周期和图象的对称轴方程;
(Ⅱ)求函数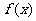 在区间
在区间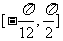 上的值域
上的值域
14.在DABC中,2sinA+cosB=2,sinB+2cosA=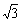 ,则ÐC的大小应为
,则ÐC的大小应为
13.若对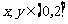 ,
,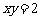 ,总有不等式
,总有不等式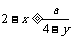 成立,则实数a的取值范围是 .
成立,则实数a的取值范围是 .
12.在抛物线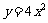 上求一点,使该点到直线
上求一点,使该点到直线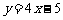 的距离为最短,该点的坐标是 .
的距离为最短,该点的坐标是 .
11.定义“等和数列”:在一个数列中,如果每一项与它的后一项的和都为同一个常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和. 已知数列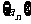 是等和数列, 且a1=2, 公和为5,那么a18的值为 ,且这个数列的前21项和S21的值为
.
是等和数列, 且a1=2, 公和为5,那么a18的值为 ,且这个数列的前21项和S21的值为
.
10.记min{a, b}=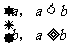 。已知
。已知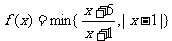 ,则
,则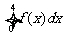 = .
= .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com