
2、下列结论正确的是( )
A、当 且
且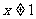 时,
时,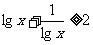 B、当
B、当 时,
时,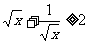
C、当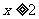 时,
时,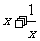 的最小值为2 D、当
的最小值为2 D、当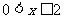 时,
时,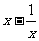 无最大值
无最大值
1、已知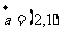 ,
,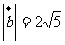 ,且
,且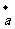 ∥
∥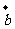 ,则
,则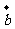 为( )
为( )
A、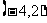 B、
B、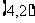 C、
C、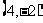 或
或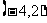 D、
D、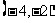 或
或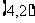
22.以下是测得的福建省某县某种产品的广告费支出x与销售额y(单位:百万元)之间,有如下的对应数据:
|
广告费支出x |
2 |
4 |
5 |
6 |
8 |
|
销售额y |
30 |
40 |
60 |
50 |
70 |
(1)画出数据对应的散点图,你能从散点图中发现福建省某县某种产品的广告费支出x与销售额y(单位:百万元)之间的一般规律吗?
(2)求y关于x的回归直线方程;
(3)预测当广告费支出为2(百万元)时,则这种产品的销售额为多少?(百万元)
21.
椭圆的中心是原点O,它的短轴长为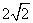 ,椭圆与双曲线
,椭圆与双曲线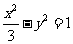 有共同的焦点
有共同的焦点
(1)求椭圆的方程;
(2),过点A(3,0)的直线与椭圆相交于不同的P、Q两点,求该直线斜率k的取值范围。
20.
已知命题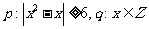 且“
且“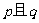 ”与“非
”与“非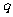 ”同时为假命题,求
”同时为假命题,求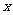 的值。
的值。
19. 摆地摊的某摊(赌)主拿了8个白的,8个黑的围棋子放在一个口袋里,并规定凡愿意摸彩者每人交一元钱作手续费,然后一次从口袋摸出5个棋子,中彩情况如下:
|
摸棋子 |
5个白 |
4个白 |
3个白 |
其它 |
|
彩金 |
20元 |
2元 |
纪念品(价值5角) |
同乐一次(无任何奖品) |
试计算:
(1)获得20元彩金的概率;
(2)获得2元彩金的概率;
(3)获得纪念品的概率;
(4)按摸彩1000次统计,赌主可望净赚多少钱?
18.设计算法:要求输入自变量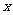 的值,输出函数
的值,输出函数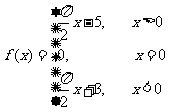 的值,并用复合if语句描述算法。
的值,并用复合if语句描述算法。
17.甲、乙两台机床在相同的技术条件下,同时生产一种零件,现在从中抽测10个,它们的尺寸分别如下(单位:mm).
甲机床:10.2 10.1 10 9.8 9.9 10.3 9.7 10 9.9 10.1;
乙机床:10.3 10.4 9.6 9.9 10.1 10.9 8.9 9.7 10.2 10.
分别计算上面两个样本的平均数和方差.如图纸规定零件的尺寸为10 mm,从计算的结果来看哪台机床加工这种零件较合适?(要求利用公式笔算)
16.已知n次多项式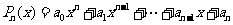 ,如果在一种算法中,计算
,如果在一种算法中,计算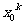 (k=2,3,4,…,n)的值需要k-1次乘法,计算
(k=2,3,4,…,n)的值需要k-1次乘法,计算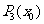 的值共需要9次运算(6次乘法,3次加法)那么计算
的值共需要9次运算(6次乘法,3次加法)那么计算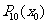 的值共需要65次运算。下面给出一种减少运算次数的算法:
的值共需要65次运算。下面给出一种减少运算次数的算法: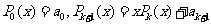 (k=0, 1,2,…,n-1).利用该算法,计算
(k=0, 1,2,…,n-1).利用该算法,计算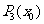 的值共需要6次运算,计算
的值共需要6次运算,计算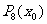 的值共需要 次运算。
的值共需要 次运算。
15. 若双曲线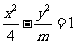 的渐近线方程为
的渐近线方程为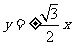 ,则双曲线的焦点坐标是_________.
,则双曲线的焦点坐标是_________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com