
19.(本小题满分12分)
已知定义在(-1,1)上的函数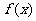 ,对于
,对于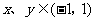 ,恒有
,恒有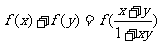 。数列{
。数列{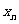 }的
}的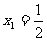 ,
,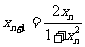 。
。
(1)求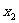 ,
,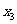 的值;
的值;
(2)(文)求证:数列{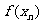 }是等比数列;
}是等比数列;
(理)求证: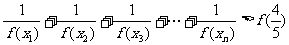
18.(本小题满分12分)
如图所示,设矩形ABCD的AB=2,AD=3,E、F分别是AD、BC的三等分点中靠近D、C的那个分点,G为CD边上的一个点,将此矩形沿EF折成直二面角。
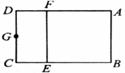
(1)当平面BFG⊥平面BEG时,求G点的位置;
(2)在(1)的前提下,求直线GE与平面BFG所成的角。
17.(本小题满分12分)
已知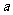 、
、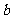 、
、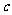 分别是△ABC的三个内角A、B、C的对边,向量
分别是△ABC的三个内角A、B、C的对边,向量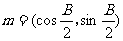 ,
,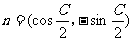 ,
,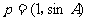 ,且
,且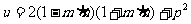 。
。
(1)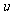 可以表示为角A的函数
可以表示为角A的函数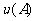 ,试
,试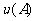 求的表达式;
求的表达式;
(2)(文)求函数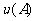 的值域;
的值域;
(理)若角A使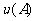 取到最大值,且
取到最大值,且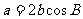 ,判断此时△ABC的形状。
,判断此时△ABC的形状。
16.已知直线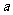 和两个平面M、N,今有三个判断:①M⊥N;②
和两个平面M、N,今有三个判断:①M⊥N;②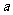 ∥M;③
∥M;③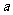 ⊥N。试以其中两个为条件,另一个为结论,写出一个正确的命题是 。
⊥N。试以其中两个为条件,另一个为结论,写出一个正确的命题是 。
15.我们把解析式相同、值域也相同,但定义域不同的几个函数叫“共生函数”。若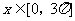 ,则解析式为
,则解析式为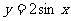 ,值域为{-1,1}的“共生函数”有 个。
,值域为{-1,1}的“共生函数”有 个。
14.在如图所示的正方形的9个格子中填入自然数(除左下角为0外,其余的均为正整数),使每一行、每一列均成等差数列,则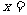 。
。
13.设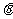 为锐角,函数
为锐角,函数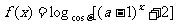 ,若
,若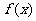 的反函数
的反函数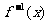 单调递增,则
单调递增,则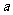 的取值范围是 。
的取值范围是 。
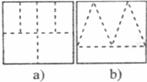
12.将一边长为4的正方形纸片按图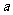 中虚线所示的方法剪开后拼成一个正四棱柱,设其体积为
中虚线所示的方法剪开后拼成一个正四棱柱,设其体积为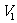 ,若将同样的正方形纸片按图
,若将同样的正方形纸片按图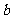 中虚线所示的方法剪开后拼成一个正四棱锥,设其体积为
中虚线所示的方法剪开后拼成一个正四棱锥,设其体积为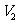 ,则
,则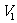 与
与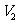 的大小关系是
的大小关系是
A.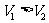 B.
B.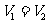 C.
C.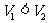 D.不确定
D.不确定
第Ⅱ卷(非选择题 共90分)
11.设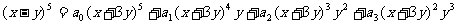
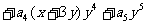 对于任意实数
对于任意实数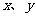 均成立,则
均成立,则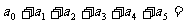
A.32 B.-32 C.243 D.-243
10.半径为4的球面上有A、B、C、D四点,且满足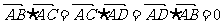 ,则△ABC、△ADB、△ACD的面积之和的最大值为
,则△ABC、△ADB、△ACD的面积之和的最大值为
A.64 B.32 C.16 D.8
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com