
(13)已知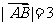 ,
,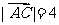 ,
,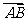 与
与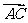 的夹角为60°,则
的夹角为60°,则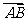 与
与 的夹角余弦为 .
的夹角余弦为 .
(14)设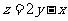 ,式中变量
,式中变量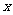 ,
,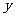 满足
满足 ,则
,则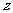 的最小值为_________.
的最小值为_________.
(15)设正四棱锥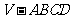 的所有棱长都是
的所有棱长都是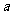 ,并且A、B、C、D、V都在一个球面上,则这个球面的面积为_______________.
,并且A、B、C、D、V都在一个球面上,则这个球面的面积为_______________.
(16)设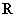 上的函数
上的函数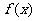 满足
满足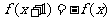 ,当
,当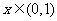 时,
时,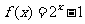 ,那么
,那么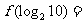 .
.
(1)函数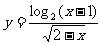 的定义域是
的定义域是
A.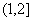 B.(1,2)
C.(2,+∞) D.(-∞,2)
B.(1,2)
C.(2,+∞) D.(-∞,2)
(2)已知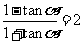 ,则
,则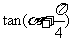 的值是
的值是
A.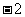 B.2 C.
B.2 C.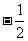 D.
D.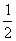
(3)设复数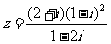 ,则z等于
,则z等于
A.2 B.-2 C.2 i D.-2 i
(4)下列各题中,使M是N成立的充要条件的一组是
A.M:a>b,N:ac2>bc2 B.M:a>b,c>d,N:a-d>b-c
C.M:a>b>0,c>d>0,N:ac>bd D.M:|a-b|=|a|+|b|,N:ab≤0
(5)函数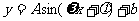 的图象如图所示,则它的解析式是
的图象如图所示,则它的解析式是
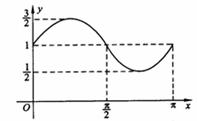
A.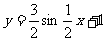 B.
B.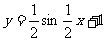
C.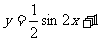 D.
D.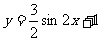
(6)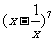 展开式的第四项等于7,则
展开式的第四项等于7,则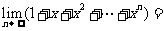
A.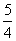 B.
B.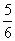 C.
C.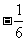 D.
D.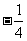
(7)设点A在圆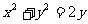 上,点B在直线
上,点B在直线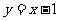 上,则|AB|的最小值是
上,则|AB|的最小值是
A.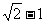 B.
B.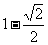 C.
C.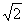 D.
D.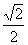
(8)设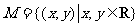 ,
,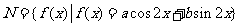 ,给出M到N的映射
,给出M到N的映射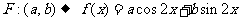 ,则点
,则点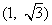 的象
的象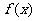 的最小正周期为
的最小正周期为
A.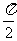 B.
B.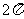 C.
C.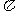 D.
D.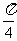
(9)设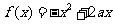 与
与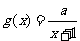 在区间
在区间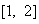 上都是减函数,则a的取值范围是
上都是减函数,则a的取值范围是
A.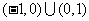 B.
B.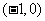 C.
C.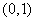 D.
D.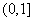
(10)由0,1,2,3,4,5六个数字组成数字不重复且百位数字不是5的5位数的个数为
A.504个 B.408个 C.720个 D.480个
(11)矩形ABCD的对角线AC、BD成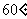 角,把矩形所在的平面以AC为折痕,折成一个直二面角D-AC-B,连结BD,则BD与平面ABC所成角的正切值为
角,把矩形所在的平面以AC为折痕,折成一个直二面角D-AC-B,连结BD,则BD与平面ABC所成角的正切值为
A.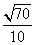 B.
B.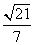 C.
C.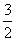 D.
D.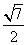
(12)已知点M(-3,0),N(3,0),B(1,0),圆C与直线MN切于点B,过M、N与圆C相切的两直线相交于点P,则P点的轨迹方程为
A.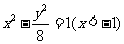 B.
B.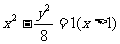
C.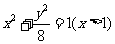 D.
D.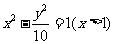
第Ⅱ卷
(17)(本小题满分10分)
已知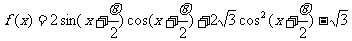 .
.
(Ⅰ)求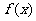 的最小正周期;
的最小正周期;
(Ⅱ)设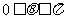 ,且函数
,且函数 为偶函数,求满足
为偶函数,求满足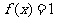 ,
,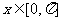 的x的集合.
的x的集合.
(18)(本小题满分12分)
有一种舞台灯,外形是正六棱柱,在其每一个侧面上安装5只颜色各异的彩灯,假若每只灯正常发光的概率为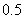 . 若一个面上至少有3只灯发光,则不需要维修,否则需要更换这个面进行维修.
. 若一个面上至少有3只灯发光,则不需要维修,否则需要更换这个面进行维修.
(Ⅰ)求一个面需要维修的概率;
(Ⅱ)求至少有3个面需要维修的概率.
(19)(本小题满分12分)如图,在正三棱柱ABC-A1B1C1中,AB=AA1,D是BC上一点,且AD⊥C1D.
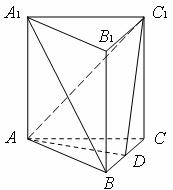
(Ⅰ)求证:A1B∥平面AC1D;
(Ⅱ)求二面角C-AC1-D的大小.
(20)(本小题满分12分)
设数列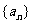 、
、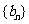 分别满足
分别满足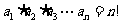 ,
,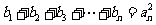 ,
,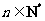 .
.
(Ⅰ)求数列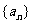 和
和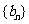 的通项公式;
的通项公式;
(Ⅱ)若数列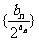 的前
的前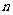 项和为
项和为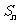 ,试求
,试求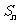 .
.
(21)(本小题满分12分)
已知函数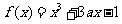 ,
,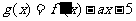 ,其中
,其中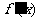 是
是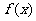 的导数.
的导数.
(Ⅰ)对满足 的一切
的一切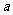 的值,都有
的值,都有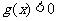 ,求实数
,求实数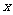 的取值范围;
的取值范围;
(Ⅱ)设直线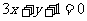 是函数
是函数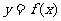 图象的一条切线,求函数
图象的一条切线,求函数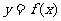 的单调区间.
的单调区间.
(22)(本小题满分12分)已知定点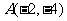 ,过点A作倾斜角为45°的直线l,交抛物线
,过点A作倾斜角为45°的直线l,交抛物线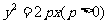 于B、C两点,且|BC|=
于B、C两点,且|BC|=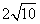 .
.
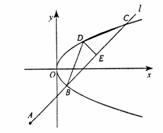
(Ⅰ)求抛物线的方程;
(Ⅱ)在(Ⅰ)中的抛物线上是否存在点D,使得|DB|=|DC|成立?如果存在,求出点D的坐标;如果不存在,请说明理由.
(13)已知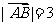 ,
,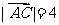 ,
,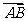 与
与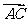 的夹角为60°,则
的夹角为60°,则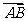 与
与 的夹角余弦为 .
的夹角余弦为 .
(14)设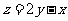 ,式中变量
,式中变量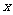 ,
,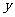 满足
满足 ,则
,则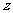 的最小值为_________.
的最小值为_________.
(15)设正四棱锥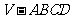 的底面ABCD在一个球的大圆上,顶点V也在这个球面上,那么它的侧面与底面所成的二面角为_______________.
的底面ABCD在一个球的大圆上,顶点V也在这个球面上,那么它的侧面与底面所成的二面角为_______________.
(16)已知定义域为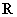 的函数
的函数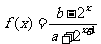 是奇函数,那么函数
是奇函数,那么函数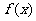 的反函数是___________________________.
的反函数是___________________________.
(1)已知全集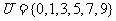 ,
,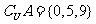 ,
,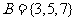 ,则
,则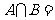
A.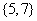 B.
B.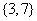 C.
C.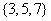 D.
D.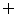
(2)若a,b是任意实数,且a>b,则
A.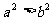 B.
B.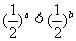 C.
C.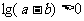 D.
D.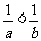
(3)已知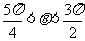 ,则
,则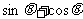 的取值范围是
的取值范围是
A.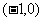 B.
B.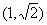 C.
C.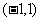 D.
D.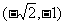
(4)在等差数列{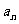 }中,若
}中,若 ,
,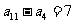 ,则
,则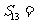
A.54 B.168 C.117 D.218
(5)函数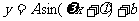 的图象如图所示,则它的解析式是
的图象如图所示,则它的解析式是
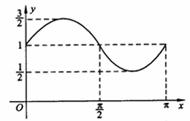
A.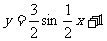 B.
B.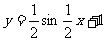
C.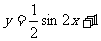 D.
D.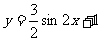
(6)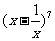 展开式的第四项等于7,则x等于
展开式的第四项等于7,则x等于
A.-5 B.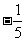
C.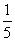 D.5
D.5
(7)经过点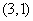 被圆C:
被圆C: 截得的弦最短的直线的方程是
截得的弦最短的直线的方程是
A.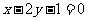 B.
B.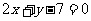
C.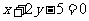 D.
D.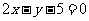
(8)4名男生与5名女生站成一排,要求4名男生的顺序一定,5名女生的顺序也一定,不同的站法总数为
A.126 B.186 C.3024 D.15120
(9)若不等式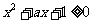 对一切
对一切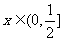 成立,那么
成立,那么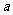 的取值范围是
的取值范围是
A.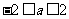 B.
B.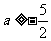 C.
C. D.
D.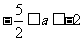
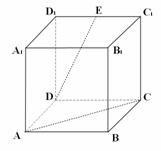
(10)如图,在棱长为2的正方体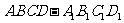 中,E是
中,E是 的中点,那么异面直线DE和AC所成的角的余弦值等于
的中点,那么异面直线DE和AC所成的角的余弦值等于
A. 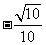 B.
B. 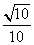
C. 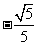 D.
D. 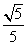
(11)函数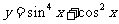 ,当
,当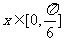 时的最小值为
时的最小值为
A.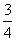 B.
B.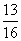 C.
C.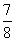 D.1
D.1
(12)已知双曲线中心在原点且一个焦点为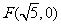 ,直线
,直线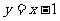 与其相交于M、N两点,MN中点的横坐标为
与其相交于M、N两点,MN中点的横坐标为 ,则此双曲线的方程是
,则此双曲线的方程是
A.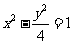 B.
B.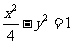 C.
C.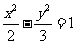 D.
D.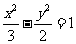
第Ⅱ卷
21.(本题满分12分)
已知函数 .
.
(Ⅰ)求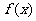 的单调区间;
的单调区间;
(Ⅱ)当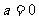 时,设斜率为
时,设斜率为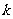 的直线与曲线
的直线与曲线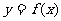 交于
交于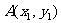 、
、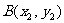
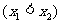 两点,求证:
两点,求证: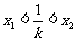 .
.
20.(本题满分14分)
已知数列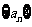 的首项
的首项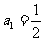 ,前
,前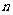 项和
项和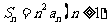 .
.
(Ⅰ)求数列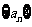 的通项公式;
的通项公式;
(Ⅱ)设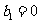 ,
,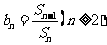 ,
,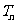 为数列
为数列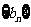 的前
的前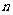 项和,求证:
项和,求证: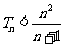 .
.
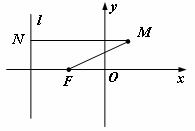
19.(本题满分14分)
已知点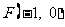 和直线
和直线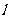 :
: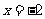 ,动点
,动点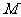 到点
到点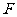 的距离与到直线
的距离与到直线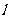 的距离之比为
的距离之比为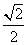 .
.
(I)求动点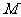 的轨迹方程;
的轨迹方程;
(II)设过点F的直线交动点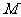 的轨迹于A、B两点,并且线段AB的中点在直线
的轨迹于A、B两点,并且线段AB的中点在直线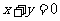 上,求直线AB的方程.
上,求直线AB的方程.
18.(本题满分14分)
在某次乒乓球比赛中,甲、乙、丙三名选手进行单循环赛(即每两个比赛一场),共比赛三场.若这三人在以往的相互比赛中,甲胜乙的概率为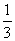 ,甲胜丙的概率为
,甲胜丙的概率为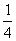 ,乙胜丙的概率为
,乙胜丙的概率为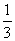 .
.
(Ⅰ)求甲获第一、丙获第二、乙获第三的概率;
(Ⅱ)若每场比赛胜者得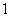 分,负者得
分,负者得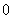 分,设在此次比赛中甲得分数为
分,设在此次比赛中甲得分数为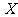 ,求
,求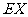 .
.
17.(本题满分14分)
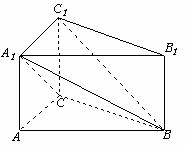
在三棱柱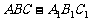 中,已知:
中,已知: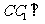 底面
底面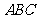 ,
,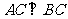 ,且
,且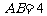 ,
,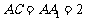 .
.
(Ⅰ)证明: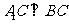 ;
;
(Ⅱ)求二面角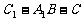 的余弦值.
的余弦值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com