
19、已知函数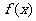 为偶函数,对任意实数
为偶函数,对任意实数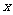 满足
满足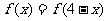 且
且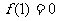 ,试分析函数
,试分析函数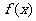 的其它性质,说明理由。
的其它性质,说明理由。
18、设集合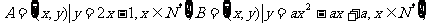 问是否存在非零整数
问是否存在非零整数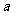 ,使
,使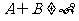 若存在,请求出
若存在,请求出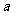 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
17、已知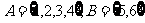 ,取适当的对应法则。
,取适当的对应法则。
(1)以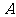 为定义域,
为定义域,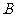 为值域的函数有多少个?
为值域的函数有多少个?
(2)在所有以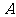 为定义域,
为定义域,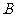 为值域的函数中,满足
为值域的函数中,满足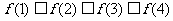 的函数有多少个?
的函数有多少个?
16、定义在R上的函数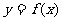 具有以下性质:①对任意实数
具有以下性质:①对任意实数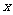 ,都有
,都有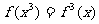 ;②对于任意
;②对于任意 .则
.则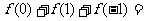 ____________________。
____________________。
15、若存在常数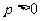 使的函数
使的函数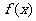 满足
满足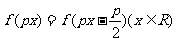 ,则
,则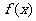 的一个周期是_______。
的一个周期是_______。
14、设函数f(n)=k(其中n∈N+),k是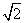 的小数点后的第n位数字,
的小数点后的第n位数字,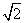 = 1.4142135623731…,则
= 1.4142135623731…,则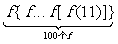 = ________
= ________
13、已知函数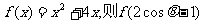 的值域是________________________.
的值域是________________________.
22、(本题14分)设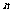 为正整数,规定:
为正整数,规定: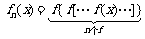 ,已知
,已知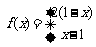
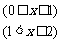 .
.
(1)解不等式: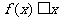 ;
;
(2)设集合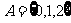 ,对任意
,对任意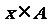 ,证明:
,证明: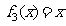 ;
;
(3)求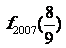 的值;
的值;
(4)若集合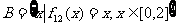 ,证明:
,证明: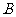 中至少包含有
中至少包含有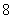 个元素.
个元素.
附加题:(开放性问题,根据问题的设计情况考虑加分,但本题总分不超过10分)
请定义集合之间的一种新运算,并举例验证这种运算是否满足交换律和结合律.
21、(本题12分)解关于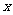 的不等式
的不等式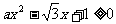
20、(本题12分)求关于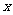 的方程
的方程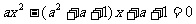 至少有一个正根的充要条件
至少有一个正根的充要条件
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com