
4.已知集合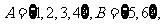 设映射
设映射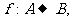 使集合B中的元素在A中都有原象,这样的映射个数共有( )
使集合B中的元素在A中都有原象,这样的映射个数共有( )
A.16个 B.15 个 C.14个 D.12个
3. 设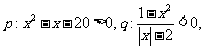 则p是q的( )
则p是q的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
2. 函数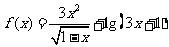 的定义域是( )
的定义域是( )
A.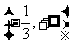 B.
B.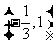 C.
C.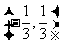 D.
D.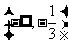
1.
设集合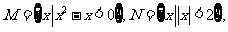 则( )
则( )
A.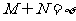 B.
B.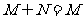 C.
C.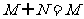 D.
D.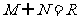
22、(本小题满分14分)已知函数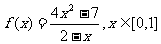 .
.
(Ⅰ)求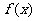 的单调区间和值域;
的单调区间和值域;
(Ⅱ)设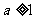 ,函数
,函数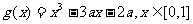 ,若对于
,若对于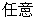
 ,总存在
,总存在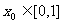 ,使得
,使得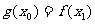 成立,求
成立,求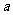 的取值范围.
的取值范围.
21、(本小题满分12分)甲、乙两个商店购进同一种商品的价格为每件30元,销售价均为每件50元。根据前5年的有关资料统计,甲商店这种商品的需求量ξ服从以下分布:
|
ξ |
10 |
20 |
30 |
40 |
50 |
|
P |
0.15 |
0.20 |
0.25 |
0.30 |
0.10 |
乙商店这种商品的需求量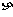 服从二项分布
服从二项分布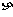 - B ( 40,0.8
).
- B ( 40,0.8
).
若这种商品在一年内没有售完,则甲商店在一年后以每件25元的价格处理。乙商店一年后剩下的这种商品第1件按25元的价格处理,第2件按24元的价格处理,第3件按23元的价格处理,依此类推。今年甲、乙两个商店同时购进这种商品40件,根据前5年的销售情况,请你预测哪间商店的期望利润较大?
20、(本小题满分12分)函数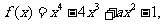 在
在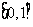 上单调递增,在
上单调递增,在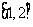 上单调递减.(1)求
上单调递减.(1)求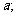 (2)函数
(2)函数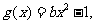 若关于
若关于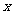 的方程
的方程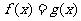 解集恰好有3个元素,求
解集恰好有3个元素,求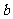 的范围.
的范围.
19、(本小题满分12分)已知数列{an}满足条件(n-1)an+1 = (n +1)(an-1)且a2 = 6 ,
设bn = an
+ n(n∈N*)
(Ⅰ)求数列{bn}的通项公式;(必须证明)
(Ⅱ)求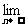 (
(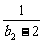 +
+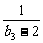 + … +
+ … +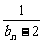 )的值
)的值
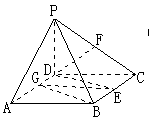
18、(本小题满分12分)在立体图形P-ABCD中,四边形ABCD是ÐDAB=60°,且边长为a的棱形,侧面PAD为正三角形,其所在平面垂直于底面ABCD。
(1)若G在AD边的中点,求证:BG^平面PAD;
(2)求证AD^PB;
(3)求二面角A-BC-P的大小;
(4)若E为BC边的中点,能否在棱PC上找到一点F,使平面DEF^平面ABCD,并证明你的结论。
17、(本小题满分12分)三支球队中,甲胜乙的概率为0.4,乙胜丙的概率为0.5,丙胜甲的概率为0.6,每场必分胜负,比赛顺序是:第一局甲对乙,第二局由第一局胜者对丙,第三局由第二局中胜者对第一局中败者,第四局是第三局胜者对第二局败者,求乙连胜四局的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com