
5、将4个颜色互不相同的球全部放入编号为1和2的两个盒子里,使得放入每个盒子里的球的个数不小于该盒子的编号,则不同的放球方法有( )
A.10种 B.20种 C.36种 D.52种
4、设集合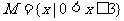 ,
,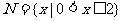 ,那么“
,那么“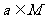 ”是“
”是“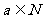 ”的( )
”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
3、设变量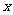 、
、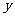 满足约束条件
满足约束条件 ,则目标函数
,则目标函数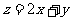 的最小值为(
)
的最小值为(
)
A.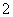 B.
B.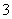 C.
C.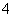 D.
D.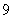
2、如果双曲线的两个焦点分别为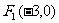 、
、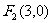 ,一条渐近线方程为
,一条渐近线方程为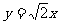 ,那么它的两条准线间的距离是( )
,那么它的两条准线间的距离是( )
A.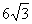 B.
B.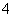 C.
C.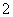 D.
D.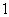
1、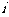 是虚数单位,
是虚数单位,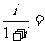 ( )
( )
A.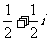 B.
B.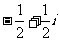 C.
C.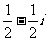 D.
D.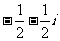
(17)(本小题满分13分)
甲、乙、丙三人在同一办公室工作。办公室只有一部电话机,设经过该机打进的电话是打给甲、乙、丙的概率依次为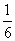 、
、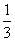 、
、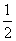 。若在一段时间内打进三个电话,且各个电话相互独立。求:
。若在一段时间内打进三个电话,且各个电话相互独立。求:
(Ⅰ)这三个电话是打给同一个人的概率;
(Ⅱ)这三个电话中恰有两个是打给甲的概率;
(18)(本小题满分13分)
设函数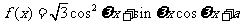 (其中
(其中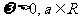 )。且
)。且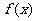 的图像在
的图像在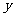 轴右侧的第一个最高点的横坐标是
轴右侧的第一个最高点的横坐标是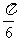 。
。
(Ⅰ)求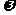 的值;
的值;
(Ⅱ)如果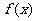 在区间
在区间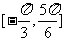 上的最小值为
上的最小值为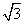 ,求
,求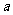 的值;
的值;
(19)(本小题满分12分)
设函数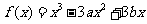 的图像与直线
的图像与直线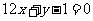 相切于点
相切于点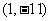 。
。
(Ⅰ)求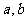 的值;
的值;
(Ⅱ)讨论函数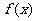 的单调性。
的单调性。
(20)(本小题满分12分)
如图,在增四棱柱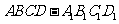 中,
中,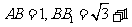 ,
,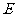 为
为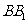 上使
上使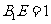 的点。平面
的点。平面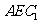 交
交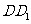 于
于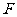 ,交
,交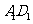 的延长线于
的延长线于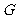 ,求:
,求:
(Ⅰ)异面直线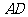 与
与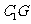 所成角的大小;
所成角的大小;
(Ⅱ)二面角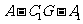 的正切值;
的正切值;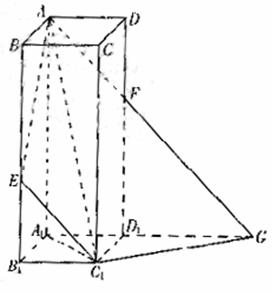
(21)(本小题满分12分)
已知定义域为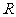 的函数
的函数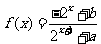 是奇函数。
是奇函数。
(Ⅰ)求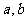 的值;
的值;
(Ⅱ)若对任意的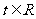 ,不等式
,不等式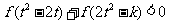 恒成立,求
恒成立,求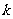 的取值范围;
的取值范围;
(22)(本小题满分12分)
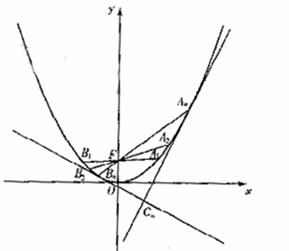
如图,对每个正整数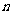 ,
,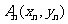 是抛物线
是抛物线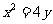 上的点,过焦点
上的点,过焦点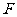 的直线
的直线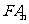 角抛物线于另一点
角抛物线于另一点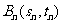 。
。
(Ⅰ)试证: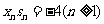 ;
;
(Ⅱ)取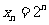 ,并记
,并记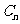 为抛物线上分别以
为抛物线上分别以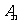 与
与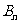 为切点的两条切线的交点。试证:
为切点的两条切线的交点。试证: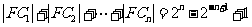 ;
;
(13)已知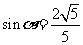 ,
,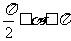 ,则
,则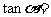 。
。
(14)在数列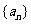 中,若
中,若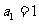 ,
,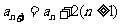 ,则该数列的通项
,则该数列的通项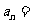 。
。
(15)设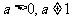 ,函数
,函数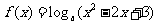 有最小值,则不等式
有最小值,则不等式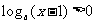 的解集为
。
的解集为
。
(16)已知变量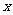 ,
,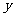 满足约束条件
满足约束条件 。若目标函数
。若目标函数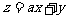 (其中
(其中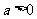 )仅在点
)仅在点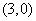 处取得最大值,则
处取得最大值,则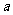 的取值范围为
。
的取值范围为
。
(A)1800 (B)3600 (C)4320 (D)5040
(10)若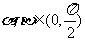 ,
,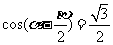 ,
,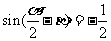 ,则
,则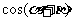 的值等于
的值等于
(A)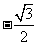 (B)
(B)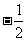 (C)
(C)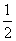 (D)
(D)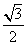
(11)设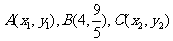 是右焦点为
是右焦点为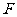 的椭圆
的椭圆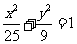 上三个不同的点,则“
上三个不同的点,则“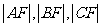 成等差数列”是“
成等差数列”是“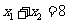 ”的
”的
(A)充要条件 (B)必要不充分条件
(C)充分不必要条件 (D)既非充分也非必要
(12)若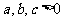 且
且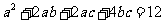 ,则
,则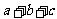 的最小值是
的最小值是
(A)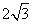 (B)3 (C)2 (D)
(B)3 (C)2 (D)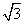
第二卷
(1)已知集合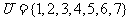 ,
,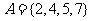 ,
,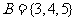 ,则
,则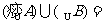
(A)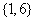 (B)
(B)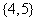 (C)
(C)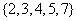 (D)
(D)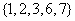
(2)在等差数列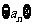 中,若
中,若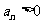 且
且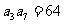 ,
,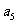 的值为
的值为
(A)2 (B)4 (C)6 (D)8
(3)以点(2,-1)为圆心且与直线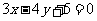 相切的圆的方程为
相切的圆的方程为
(A)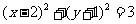 (B)
(B)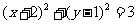
(C)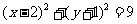 (D)
(D)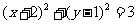
(4)若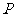 是平面
是平面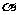 外一点,则下列命题正确的是
外一点,则下列命题正确的是
(A)过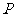 只能作一条直线与平面
只能作一条直线与平面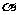 相交 (B)过
相交 (B)过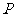 可作无数条直线与平面
可作无数条直线与平面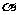 垂直
垂直
(C)过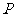 只能作一条直线与平面
只能作一条直线与平面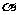 平行 (D)过
平行 (D)过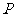 可作无数条直线与平面
可作无数条直线与平面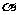 平行
平行
(5)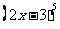 的展开式中
的展开式中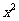 的系数为
的系数为
(A)-2160 (B)-1080 (C)1080 (D)2160
(6)设函数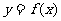 的反函数为
的反函数为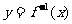 ,且
,且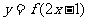 的图像过点
的图像过点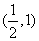 ,则
,则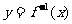 的图像必过
的图像必过
(A)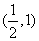 (B)
(B)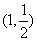 (C)
(C)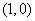 (D)
(D)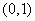
(7)某地区有300家商店,其中大型商店有30家,中型商店有75家,小型商店有195家。为了掌握各商店的营业情况,要从中抽取一个容量为20的样本。若采用分层抽样的方法,抽取的中型商店数是
(A)2 (B)3 (C)5 (D)13
(8)已知三点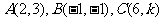 ,其中
,其中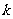 为常数。若
为常数。若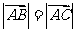 ,则
,则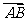 与
与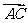 的夹角为
的夹角为
(A)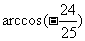 (B)
(B)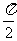 或
或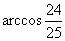
(C)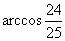 (D)
(D)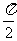 或
或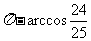
(17)(本小题满分13分)
设函数f(x)=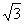 cos2cos+sin
cos2cos+sin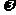 rcos
rcos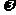 x+a(其中
x+a(其中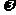 >0,a
>0,a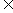 R),且f(x)的图象在y轴右侧的第一个高点的横坐标为
R),且f(x)的图象在y轴右侧的第一个高点的横坐标为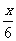 .
.
(Ⅰ)求ω的值;
(Ⅱ)如果f(x)在区间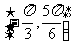 上的最小值为
上的最小值为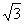 ,求a的值.
,求a的值.
(18)(本小题满分13分)
某大厦的一部电梯从底层出发后只能在第18、19、20层可以停靠.若该电梯在底层载有 5位乘客,且每位乘客在这三层的每一层下电梯的概率均为
5位乘客,且每位乘客在这三层的每一层下电梯的概率均为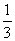 ,用ξ表示这5位乘客在第20层下电梯的人数.求:
,用ξ表示这5位乘客在第20层下电梯的人数.求:
(Ⅰ)随机变量ξ的分布列;
(Ⅱ)随机变量ξ的期望.
(19)(本小题满分13分)
如图,在四棱锥P-ABCD中,PA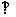 底面ABCD,
底面ABCD, DAB为直角,AB‖CD,AD=CD=24B,E、F分别为PC、CD的中点.
DAB为直角,AB‖CD,AD=CD=24B,E、F分别为PC、CD的中点.
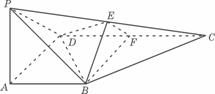
图(19)图
(Ⅰ)试证:CD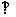 平面BEF;
平面BEF;
(Ⅱ)设PA=k·AB,且二面角E-BD-C的平面角大于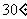 ,求k的取值范围.
,求k的取值范围.
(20)(本小题满分13分)
已知函数f(x)=(x2+bx+c)cx,其中b,c R为常数.
R为常数.
(Ⅰ)若b2>4(a-1),讨论函数f(x)的单调性;
(Ⅱ)若b2<4(c-1),且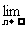
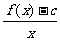 =4,试证:-6≤b≤2.
=4,试证:-6≤b≤2.
(21)(本小题满分12分)
已知定义域为R的函数f(x)满足f(f(x)-x2+y_=f(x)-x2+x.
(Ⅰ)若f(2)-3,求f(1);又若f(0)=a,求f(a);
(Ⅱ)设有且仅有一个实数x0,使得f(x0)= x0,求函数f(x)的解析表达式.
(22)(本小题满分12分)
已知一列椭圆Cn:x2+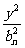 =1.
0<bn<1,n=1,2.
=1.
0<bn<1,n=1,2. .若椭圆C上有一点Pn使Pn到右准线ln的距离d.是|PnFn|与|PnCn|的等差中项,其中Fn、Cn分别是Cn的左、右焦点.
.若椭圆C上有一点Pn使Pn到右准线ln的距离d.是|PnFn|与|PnCn|的等差中项,其中Fn、Cn分别是Cn的左、右焦点.
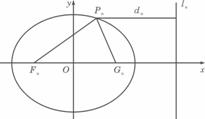
(Ⅰ)试证:bn≤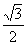 (n≥1);
(n≥1);
(Ⅱ)取bn=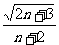 ,并用SA表示
,并用SA表示 PnFnGn的面积,试证:S1<S1且Sn<Sn+3 (n≥3).
PnFnGn的面积,试证:S1<S1且Sn<Sn+3 (n≥3).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com