
22.(本题满分18分)本题共有3个小题,第1小题满分3分,第2小题满分6分,第3小题满分9分)
已知函数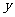 =
=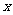 +
+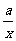 有如下性质:如果常数
有如下性质:如果常数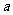 >0,那么该函数在
>0,那么该函数在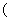 0,
0,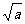
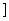 上是减函数,在
上是减函数,在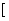
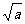 ,+∞
,+∞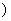 上是增函数.
上是增函数.
(1)如果函数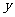 =
=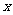 +
+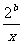 (
(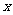 >0)的值域为
>0)的值域为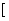 6,+∞
6,+∞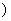 ,求
,求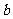 的值;
的值;
(2)研究函数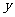 =
=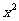 +
+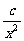 (常数
(常数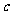 >0)在定义域内的单调性,并说明理由;
>0)在定义域内的单调性,并说明理由;
(3)对函数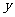 =
=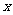 +
+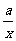 和
和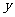 =
=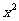 +
+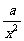 (常数
(常数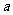 >0)作出推广,使它们都是你所推广的函数的特例.研究推广后的函数的单调性(只须写出结论,不必证明),并求函数
>0)作出推广,使它们都是你所推广的函数的特例.研究推广后的函数的单调性(只须写出结论,不必证明),并求函数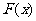 =
=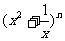 +
+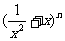 (
(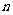 是正整数)在区间[
是正整数)在区间[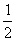 ,2]上的最大值和最小值(可利用你的研究结论).
,2]上的最大值和最小值(可利用你的研究结论).
[解]
21.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分)
已知有穷数列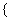
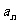
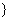 共有2
共有2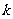 项(整数
项(整数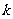 ≥2),首项
≥2),首项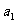 =2.设该数列的前
=2.设该数列的前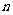 项和为
项和为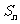 ,且
,且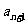 =
=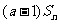 +2(
+2(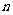 =1,2,┅,2
=1,2,┅,2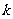 -1),其中常数
-1),其中常数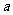 >1.
>1.
(1)求证:数列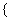
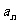
 是等比数列;
是等比数列;
(2)若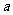 =2
=2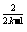 ,数列
,数列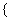
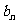
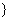 满足
满足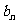 =
=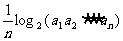 (
(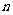 =1,2,┅,2
=1,2,┅,2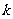 ),求数列
),求数列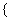
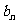
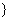 的通项公式;
的通项公式;
(3)若(2)中的数列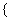
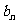
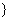 满足不等式|
满足不等式|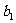 -
-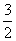 |+|
|+|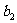 -
-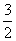 |+┅+|
|+┅+|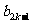 -
-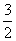 |+|
|+|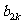 -
-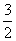 |≤4,求
|≤4,求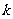 的值.
的值.
[解]
20.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分)
在平面直角坐标系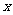 O
O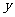 中,直线
中,直线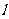 与抛物线
与抛物线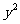 =2
=2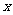 相交于A、B两点.
相交于A、B两点.
(1)求证:“如果直线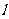 过点T(3,0),那么
过点T(3,0),那么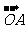
 =3”是真命题;
=3”是真命题;
(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由.
[解]
19.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分)
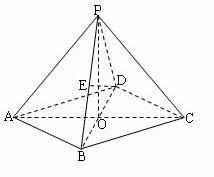
如图所示:在四棱锥P-ABCD中,底面是边长为2的菱形,∠DAB=60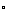 ,对角线AC与BD相交于点O,PO⊥平面ABCD,PB与平面ABCD所成的角为60
,对角线AC与BD相交于点O,PO⊥平面ABCD,PB与平面ABCD所成的角为60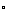 .
.
(1)求四棱锥P-ABCD的体积;
(2)若E是PB的中点,求异面直线DE与PA所成角的大小(结果用反三角函数值表示).
[解]
18.(本题满分12分)
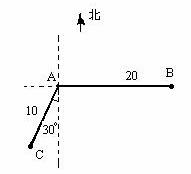
如图,当甲船位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待营救.甲船立即前往救援,同时把消息告知在甲船的南偏西30 ,相距10海里C处的乙船,试问乙船应朝北偏东多少度的方向沿直线前往B处救援(角度精确到1
,相距10海里C处的乙船,试问乙船应朝北偏东多少度的方向沿直线前往B处救援(角度精确到1 )?
)?
[解]
17.(本题满分12分)
求函数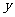 =2
=2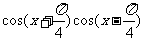 +
+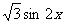 的值域和最小正周期.
的值域和最小正周期.
[解]
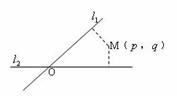
16.如图,平面中两条直线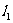 和
和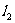 相交于点O,对于平面上任意一点M,若
相交于点O,对于平面上任意一点M,若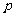 、
、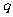 分别是M到直线
分别是M到直线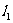 和
和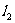 的距离,则称有序非负实数对(
的距离,则称有序非负实数对(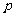 ,
,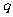 )是点M的“距离坐标”.已知常数
)是点M的“距离坐标”.已知常数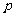 ≥0,
≥0,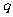 ≥0,给出下列命题:
≥0,给出下列命题:
①若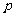 =
=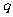 =0,则“距离坐标”为(0,0)的点有且仅有1个;
=0,则“距离坐标”为(0,0)的点有且仅有1个;
②若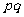 =0,且
=0,且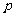 +
+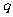 ≠0,则“距离坐标”为(
≠0,则“距离坐标”为(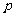 ,
,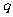 )的点有且仅有2个;
)的点有且仅有2个;
③若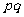 ≠0,则“距离坐标”为(
≠0,则“距离坐标”为(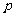 ,
,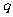 )的点有且仅有4个.
)的点有且仅有4个.
上述命题中,正确命题的个数是 ( )
(A)0; (B)1; (C)2; (D)3.
第二卷
15.若关于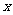 的不等式
的不等式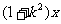 ≤
≤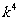 +4的解集是M,则对任意实常数
+4的解集是M,则对任意实常数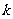 ,总有( )
,总有( )
(A)2∈M,0∈M; (B)2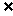 M,0
M,0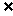 M; (C)2∈M,0
M; (C)2∈M,0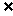 M; (D)2
M; (D)2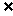 M,0∈M.
M,0∈M.
14.若空间中有四个点,则“这四个点中有三点在同一直线上”是“这四个点在同一平面上”的 ( )
(A)充分非必要条件;(B)必要非充分条件;(C)充要条件;(D)非充分非必要条件.
13.在平行四边形ABCD中,下列结论中错误的是 ( )
(A)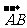 =
=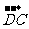 ;(B)
;(B)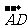 +
+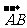 =
=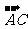 ;
;
(C)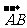 -
-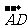 =
=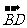 ;(D)
;(D)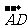 +
+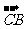 =
=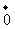 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com