
5.在正四面体P-ABC中,D,E,F分别是AB,BC,CA的中点,下面四个结论中不成立的是
A.平面PDF⊥平面ABC B.DF⊥平面PAE
C.BC//平面PDF D.平面PAE⊥平面ABC
4、已知数列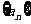 满足
满足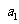 =1,
=1,
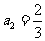 且
且 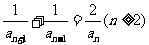 , 则
, 则 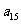 等于
等于
(A) (B) (C) (D)
3.设直线ax+by+c=0的倾斜角为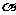 ,且sin
,且sin cos
cos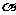 =0,则a,b满足(
)
=0,则a,b满足(
)
A.a+b=1 B.a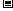 b=1 C.a+b=0 D.a
b=1 C.a+b=0 D.a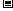 b=0
b=0
2、D是△ABC的边AB上靠近A点的三等分点,则向量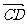 等于( )
等于( )
A 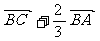 B
B 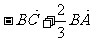 C
C 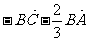 D
D 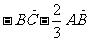
1.sin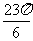 的值是( )
的值是( )
A.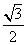 B.
B.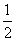 C.
C.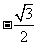 D.
D.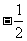
22.(本题满分14分)设二次函数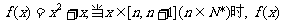 的函数值的所有整数值的个数为
的函数值的所有整数值的个数为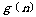 .
.
(Ⅰ) 求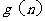 的表达式.
的表达式.
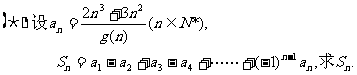
(Ⅲ) 设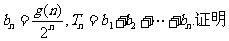 :
: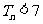 。
。
20、(本题满分12分)
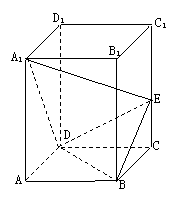 如图,已知直平行六面体ABCD-A1B1C1D1中,AD⊥BD,AD=BD=a,E是CC1的中点,A1D⊥BE.
如图,已知直平行六面体ABCD-A1B1C1D1中,AD⊥BD,AD=BD=a,E是CC1的中点,A1D⊥BE.
(I)求证:A1D⊥平面BDE;
(II)求二面角B―DE―C的大小;
(III)求点B到平面A1DE的距离
21(本题满分12分)如图,摩天轮的半径为40m,摩天轮的圆心O点距地面的高度为50m,摩天轮做匀速转动,每3min转一圈,摩天轮上的点P的起始位置在最低点处。
(1) 已知在时刻t(min)时点P距离地面的高度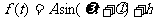 ,求2006min时点P距离地面的高度
,求2006min时点P距离地面的高度
(2) 求证:不论t为何值,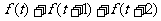 是定值
是定值
19、(本题满分12分)(1)若圆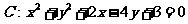 ,已知不过原点的直线
,已知不过原点的直线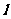 与圆
与圆 相切,且在两坐标上的截距相等,求直线
相切,且在两坐标上的截距相等,求直线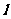 的方程;(2)求圆心在直线
的方程;(2)求圆心在直线 ,并且与直线
,并且与直线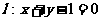 相切于点
相切于点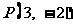 的圆的方程
的圆的方程
18. (本题满分12分)已知函数f(x)=sin(x+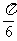 )+sin(x-
)+sin(x-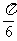 )+cosx+a(a∈R,a为常数).
)+cosx+a(a∈R,a为常数).
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)若函数f(x)在[-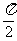 ,
,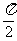 ]上的最大值与最小值之和为
]上的最大值与最小值之和为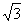 ,求实数a的值.
,求实数a的值.
17.(本题满分12分)已知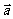 、
、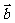 、
、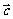 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中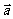
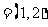 .
.
(1) 若 |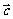 |=2,且
|=2,且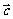 //
//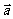 ,求
,求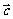 的坐标;
的坐标;
(2) 若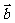
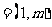
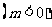 且
且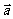 +2
+2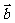 与
与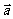 -2
-2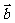 垂直,求
垂直,求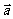 与
与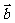 的夹角
的夹角 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com