
6.已知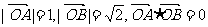 ,点C在∠AOB内,且∠AOC=45°,设
,点C在∠AOB内,且∠AOC=45°,设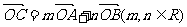 ,则
,则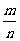 等于 ( )
等于 ( )
A.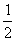 B.
B.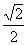 C.
C.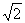 D.2
D.2
 7.把函数
7.把函数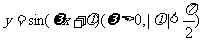 的图象按向量
的图象按向量
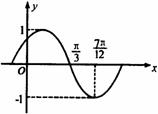
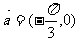 平移,所得曲线的一部分如图所示,则ω,
平移,所得曲线的一部分如图所示,则ω,
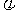 的值分别是( )
的值分别是( )
A.1,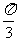 B.1,-
B.1,-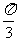
C.2,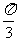 D.2,-
D.2,-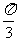
5.若数列{an}满足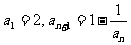 ,则a2007的值 ( )
,则a2007的值 ( )
A.1 B.-1 C.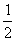 D.2
D.2
4.若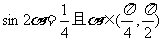 ,则
,则 的值是 ( )
的值是 ( )
A.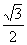 B.
B.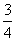 C.-
C.-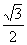 D.-
D.-
3.若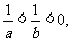 则下列不等式:①
则下列不等式:①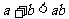 ②
②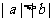 ③
③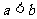 ④
④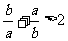 中,正确的不等式有 ( )
中,正确的不等式有 ( )
A.①② B.②③ C.①④ D.③④
2.已知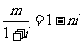 ,其中m,n是实数,是m+ni等于 ( )
,其中m,n是实数,是m+ni等于 ( )
A.1+2i B.1-2i C.2+i D.2-i
1.设P、Q为两个非空实数集合,定义集合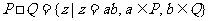 ,若P={-1,0,1},Q={-2,2},则集合
,若P={-1,0,1},Q={-2,2},则集合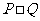 中元素的个数是 ( )
中元素的个数是 ( )
A.3 B.4 C.5 D.6
22.(本小题满分14分)
对于数列{an},定义{△an }为数列{an}的一阶差分数列,其中
(1)若数列{an}的通项公式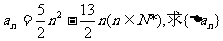 的通项公式;
的通项公式;
(2)若数列{an}的首项是1,且满足 ,
,
①证明数列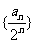 为等差为数列;
为等差为数列;
②求{an}的前n项和Sn
21.(本小题满分12分)
学校食堂定期从某粮店以每吨1500元的价格买大米,每次购进大米需支付运输劳务费100元,已知食堂每天需要大米1吨,贮存大米的费用为每吨每天2元,假定食堂每次均在用完大米的当天购买。
(1)该食堂每多少天购买一次大米,能使平均每天所支付的费用最少?
(2)粮店提出价格优惠条件:一次购买量不少于20吨时,大米价格可享受九五折优惠(即是原价的95%),问食堂可否接受此优惠条件?请说明理由。
20.(本小题满分12分)
已知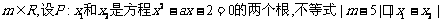 对任意实数a∈[1,2]恒成立;Q:函数
对任意实数a∈[1,2]恒成立;Q:函数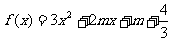 有两个不同的零点.求使“P且Q”为真命题的实数m的取值范围.
有两个不同的零点.求使“P且Q”为真命题的实数m的取值范围.
19.(本小题满分12分)
已知定义在R上奇函数,当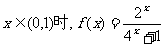
(1)求f(x)在(-1,1)上的解析式
(2)证明f(x)在(0,1)上是减函数
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com