
1、设集合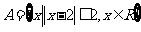 ,
,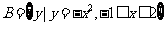 ,则
,则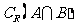 等于
等于
A.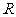 B.
B.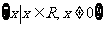 C.
C.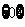 D.
D.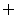
22、(本小题满分14分)已知数列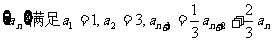
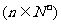
(1)证明:数列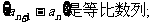
(2)求数列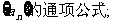
(3)若数列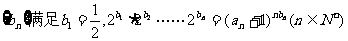
求证: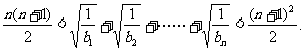
21、(本小题满分12分)
设函数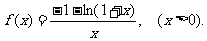
(Ⅰ)函数f (x)在(0,+∞)上是增函数还是减函数,并证明你的结论
(Ⅱ)若当x >0时,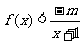 恒成立,求正整数m的最大值
恒成立,求正整数m的最大值
20、(本小题满分12分)
已知: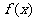 为定义在
为定义在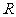 上的奇函数,且当
上的奇函数,且当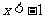 时,
时,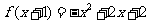 。
。
(1)写出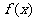 的函数表达式;(2)作出函数
的函数表达式;(2)作出函数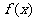 的图象,并求出
的图象,并求出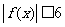 的解集;
的解集;
19、(本小题满分12分)
某厂生产某种产品的年固定成本为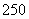 万元,每生产
万元,每生产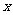 千件,需另投入成本为
千件,需另投入成本为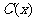 ,当年产量不足
,当年产量不足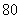 千件时,
千件时,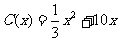 (万元);当年产量不小于
(万元);当年产量不小于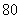 千件时,
千件时,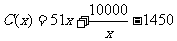 (万元).通过市场分析,若每件售价为
(万元).通过市场分析,若每件售价为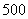 元时,该厂年内生产该商品能全部销售完.
元时,该厂年内生产该商品能全部销售完.
(1)写出年利润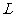 (万元)关于年产量
(万元)关于年产量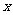 (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
18、(本小题满分12分,)
在等比数列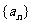 中,
中,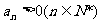 ,公比
,公比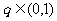 ,且
,且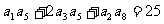 ,又
,又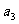 与
与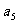 的等比中项为
的等比中项为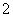 ,
,
(1)求数列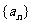 的通项公式;
的通项公式;
(2)设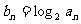 ,数列
,数列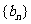 的前
的前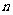 项和为
项和为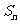 ,当
,当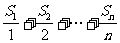 最大时,求
最大时,求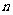 的值.
的值.
17、(本小题满分12分)
设函数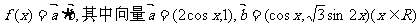
(Ⅰ)求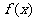 的最小正周期
的最小正周期
(Ⅱ)在△ABC中,a,b,c分别是角A,B,的对边,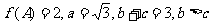
求b,c的长
16、水池有两个相同的进水口和一个出水口,每个口进出水速度如图甲、乙所示,某天O点到6点该水池的蓄水量如图丙所示(至少打开一个水口):
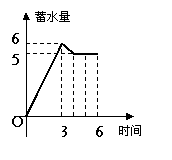
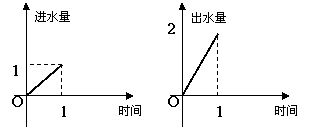
甲 乙 丙
给出以下3个论断:①O点到3点只进水不出水;②3点到4点不进水只出水;③4点到6点不进水也不出水.
则一定正确的论断是 .
15、已知数列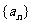 满足
满足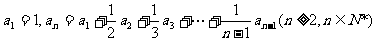 .
.
若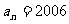 ,则
,则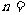 ____
____
14、已知函数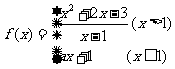 连续,则a的值为 。
连续,则a的值为 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com