
6.已知圆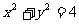 与圆
与圆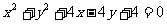 关于直线
关于直线 对称,则直线
对称,则直线 的方程
的方程
(A) 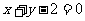 (B)
(B) 
(C)  (D)
(D) 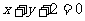
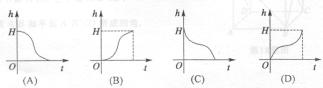
5.如图,盛满清水的花瓶的高为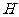 ,其底部碰破了一个小洞,满瓶水从洞中匀速流出.花瓶中水面的高度
,其底部碰破了一个小洞,满瓶水从洞中匀速流出.花瓶中水面的高度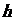 随时间
随时间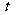 变化的图象与下列哪个图象相符合
变化的图象与下列哪个图象相符合

4.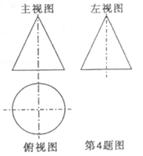 如图,一个空间几何体的主视图和左视图都是边长为1 的正三角形,俯视图是一个圆,那么这个几何体的表面积为
如图,一个空间几何体的主视图和左视图都是边长为1 的正三角形,俯视图是一个圆,那么这个几何体的表面积为
(A)
(B)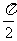
(C)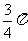
(D) 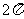
3.下列各组函数中,表示同一函数的有( )组
①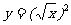 ,
,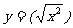 ;②
;②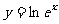 ,
,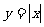 ;
;
③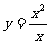 ,
,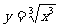 ;④
;④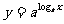 ,
,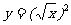 .
.
(A) O (B) l
(C) 2 (D) 3
(A) 1 (B) 2 (C) 3 (D)4
2.过点(3,2)
,且与直线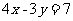 垂直的直线的方程是
垂直的直线的方程是
(A) 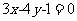 (B)
(B) 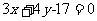
(C) 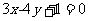 (D)
(D)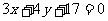
(17)(本小题满分12分)
在 ABC中,
ABC中,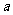 、
、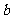 、
、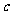 分别是A、B、C的对边. 若向量m=(2, 0)与n=(
分别是A、B、C的对边. 若向量m=(2, 0)与n=(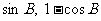 )所成角为
)所成角为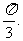
(I) 求角B的大小;
(II)若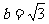 ,求
,求 的最大值.
的最大值.
(18)(本小题满分12分)
某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
|
|
积极参加班级工作 |
不太主动参加班级工作 |
合计 |
|
学习积极性高 |
18 |
7 |
25 |
|
学习积极性一般 |
6 |
19 |
25 |
|
合 计 |
24 |
26 |
50 |
(I)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太积极参加班级工作且学习积极性一般的学生的概率是多少?
(II)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关?并说明理由.
(19)(本小题满分12分)
已知数列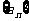 的前项n和为
的前项n和为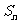 ,对一切正整数n,点(n,
,对一切正整数n,点(n, 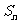 )都在函数
)都在函数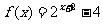 的图象上.
的图象上.
(I) 求数列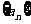 的通项公式;
的通项公式;
(II)设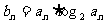 ,求数列
,求数列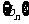 的前n项的和
的前n项的和
 (20)(本小题满分12分)
(20)(本小题满分12分)
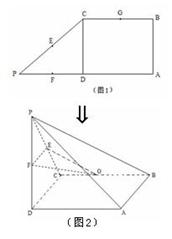
如图1,在直角梯形ABCP中,AP//BC,AP⊥AB,AB=BC=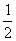 AP=2,D为AP的中点,E,F,G分别为PC、PD、CB的中点,将
AP=2,D为AP的中点,E,F,G分别为PC、PD、CB的中点,将 PCD沿CD折起,使点P在平面ABCD上的射影为点D,如图2.
PCD沿CD折起,使点P在平面ABCD上的射影为点D,如图2.
(I)求证:AP//平面EFG;
(II)求三棱锥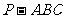 的体积.
的体积.
(21)(本小题满分12分)
 如图中心在原点,焦点在
如图中心在原点,焦点在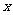 轴上的椭圆,离心率
轴上的椭圆,离心率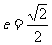 ,且经过抛物线
,且经过抛物线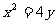 的焦点.
的焦点.
(I)求椭圆的标准方程;
(II)若过点B的直线 (斜率不等于零)与椭圆交于不同的两点E、F(E在B、F之间),试求
(斜率不等于零)与椭圆交于不同的两点E、F(E在B、F之间),试求 OBE与
OBE与 OBF面积之比的取值范围.
OBF面积之比的取值范围.
(22) (本小题满分14分)
设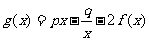 ,其中
,其中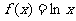 ,且
,且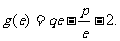 (
(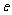 为自然对数的底数)
为自然对数的底数)
(I)求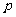 与
与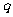 的关系;
的关系;
(II)若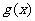 在其定义域内为单调函数,求
在其定义域内为单调函数,求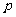 的取值范围;
的取值范围;
(III)证明:
① 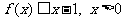 ;
;
② 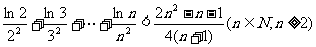 .
.
(13)若点P(3,1)是圆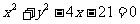 的弦AB的中点,则直线AB的方程是 .
的弦AB的中点,则直线AB的方程是 .
(14)设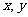 为正数,且
为正数,且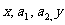 成等差数列,
成等差数列,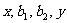 成等比数列,则
成等比数列,则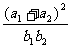 的最小值是
.
的最小值是
.
(15)在样本的频率分布直方图中,共有4个小长方形,这4个小长方形的面积由小到大构成等差数列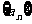 ,已知
,已知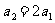 ,且样本容量为400,则小长方形面积最大的一组的频数 为
.
,且样本容量为400,则小长方形面积最大的一组的频数 为
.
(16)对于函数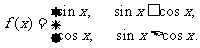 给出下列四个命题:
给出下列四个命题:
① 该函数是以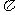 为最小正周期的周期函数;
为最小正周期的周期函数;
② 当且仅当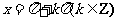 时,该函数取得最小值是-1;
时,该函数取得最小值是-1;
③ 该函数的图象关于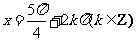 对称;
对称;
④当且仅当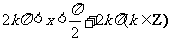 时,
时,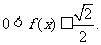
其中正确命题的序号是 (请将所有正确命题的序号都填上)
(1)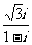 的共轭复数是
的共轭复数是
(A)
-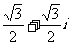 (B)
(B)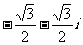 (C)
(C)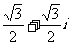 (D)
(D)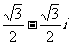
(2)已知条件P: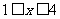 ,条件
,条件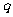 :
: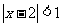 ,则
,则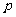 是
是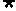
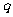 的
的
 (A)充分不必要条件
(B)必要不充分条件
(A)充分不必要条件
(B)必要不充分条件
(C)充要条件 (D)既非充分也非必要条件
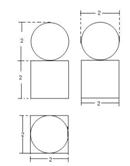
(3)一个几何体的三视图如图所示,则该几何体的体积等于
(A)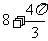 (B)
(B) 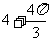
(C)  (D)
(D) 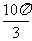
(4) 在一底面半径和高都是2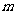 的圆柱形容器中盛满小麦,但有一粒带麦锈病的种子混入了其中. 现从中随机取出2
的圆柱形容器中盛满小麦,但有一粒带麦锈病的种子混入了其中. 现从中随机取出2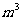 的种子,则取出带麦锈病种子的概率是
的种子,则取出带麦锈病种子的概率是
(A)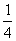 (B)
(B)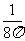 (C)
(C) 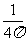 (D) 1-
(D) 1-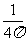
(5)设F是椭圆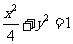 的右焦点,椭圆上的点与点F的最大距离为M,最小距离是m,则椭圆上与点F的距离是
的右焦点,椭圆上的点与点F的最大距离为M,最小距离是m,则椭圆上与点F的距离是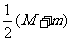 的点的坐标是
的点的坐标是
(A) (0,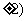 (B)
(B)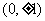 (C)
(C)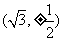 (D)
(D) 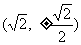
(6)已知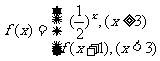 , 则
, 则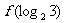 的值是
的值是
 (A)
(A)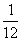 (B)
(B)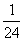 (C)
24
(D) 12
(C)
24
(D) 12
(7)如图,程序框图所进行的求和运算是
(A)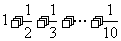
(B)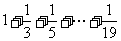
(C)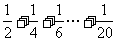
(D)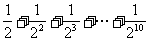
(8)设双曲线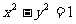 的两条渐近线与直线
的两条渐近线与直线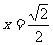 围成的三角形区域(包含边界)为D, P(
围成的三角形区域(包含边界)为D, P(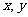 )为D内的一个动点,则目标函数
)为D内的一个动点,则目标函数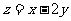 的最小值为
的最小值为
(A)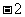 (B)
(B)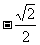 (C)0 (D)
(C)0 (D)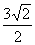
(9)设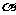 、
、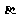 、
、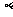 为平面,
为平面,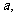
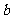 为直线,给出下列条件
为直线,给出下列条件
① 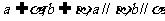 ;
;
② 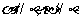 ;
;
③ 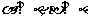 ;
;
④ 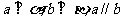
其中能使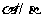 成立的条件是
成立的条件是
(A)①② (B) ②③ (C) ② ④ (D) ③④
(10) 已知幂函数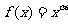 的部分对应值如下表:
的部分对应值如下表:
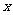 |
1 |
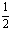 |
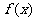 |
1 |
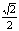 |
则不等式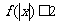 的解集是
的解集是
(A)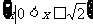 (B)
(B)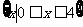 (C)
(C)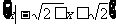 (D)
(D) 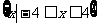
(11)在股票买卖过程中,经常用到两种曲线,一种是即时价格曲线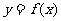 , 另一种是平均价格曲线
, 另一种是平均价格曲线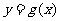 (如f(2)=3是价格开始买卖后2小时的即时价格为3元;g(2)=3表示2小时内的平均价格为3元),下面给出了四个图象,其中实线表示y=f(x),虚线表示y=g(x),其中可能正确的是
(如f(2)=3是价格开始买卖后2小时的即时价格为3元;g(2)=3表示2小时内的平均价格为3元),下面给出了四个图象,其中实线表示y=f(x),虚线表示y=g(x),其中可能正确的是
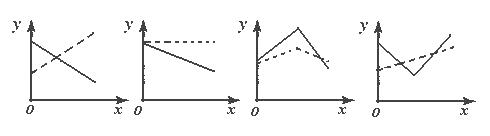
(A) (B) (C) (D)
(12)已知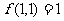 ,
,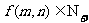 (
(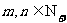 )且对任意
)且对任意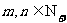 都有
都有
① 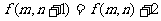 ;
;
② 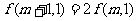 .
.
则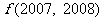 的值为
的值为
(A)  (B)
(B) (C)
(C) (D)
(D)
(17)(本小题满分12分)
在 ABC中,
ABC中,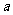 、
、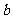 、
、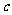 分别是A、B、C的对边. 若向量m=(2, 0)与n=(
分别是A、B、C的对边. 若向量m=(2, 0)与n=(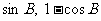 )所成角为
)所成角为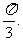
(I) 求角B的大小;
(II)若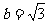 ,求
,求 的最大值.
的最大值.
(18)(本小题满分12分)
已知数列的前项n和为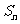 ,对一切正整数n,点(n,
,对一切正整数n,点(n, 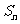 )都在函数
)都在函数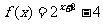 的图象上.
的图象上.
(I) 求数列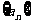 的通项公式;
的通项公式;
(II)设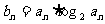 ,求数列
,求数列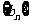 的前n项的和
的前n项的和
 (19)(本小题满分12分)
(19)(本小题满分12分)
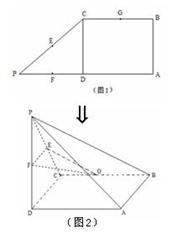
如图1,在直角梯形ABCP中,AP//BC,AP⊥AB,AB=BC=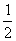 AP=2,D为AP的中点,E,F,G分别为PC、PD、CB的中点,将
AP=2,D为AP的中点,E,F,G分别为PC、PD、CB的中点,将 PCD沿CD折起,使点P在平面ABCD上的射影为点D,如图2.
PCD沿CD折起,使点P在平面ABCD上的射影为点D,如图2.
(I)求证:AP//平面EFG;
(II)求二面角E-FG-D的一个三角函数值.
(20)(本小题满分12分)
某次象棋比赛的决赛在甲乙两名棋手之间举行,比赛采用积分制,比赛规则规定赢一局得2分,平一局得1分,输一局得0分;比赛共进行五局,积分有超过5分者比赛结束,否则继续进行. 根据以往经验,每局甲赢的概率为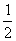 ,乙赢的概率为
,乙赢的概率为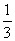 ,且每局比赛输赢互不受影响. 若甲第n局赢、平、输的得分分别记为
,且每局比赛输赢互不受影响. 若甲第n局赢、平、输的得分分别记为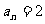 、
、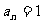 、
、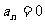
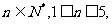 令
令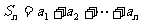 .
.
(Ⅰ)求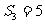 的概率;
的概率;
(Ⅱ)若随机变量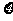 满足
满足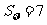 (
(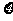 表示局数),求
表示局数),求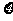 的分布列和数学期望.
的分布列和数学期望.
(21)(本小题满分12分)
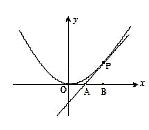 如图,已知直线
如图,已知直线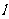 与抛物线
与抛物线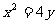 相切于点P(2, 1),且与
相切于点P(2, 1),且与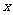 轴交于点A,定点B的坐标为(2, 0) .
轴交于点A,定点B的坐标为(2, 0) .
(I)若动点M满足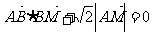 ,求点M的轨迹C;
,求点M的轨迹C;
(II)若过点B的直线 (斜率不等于零)与(I)中的轨迹C交于不同的两点E、F(E在B、F之间),试求
(斜率不等于零)与(I)中的轨迹C交于不同的两点E、F(E在B、F之间),试求 OBE与
OBE与 OBF面积之比的取值范围.
OBF面积之比的取值范围.
(22) (本小题满分14分)
设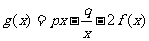 ,其中
,其中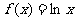 ,且
,且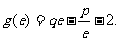 (
(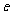 为自然对数的底数)
为自然对数的底数)
(I)求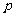 与
与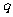 的关系;
的关系;
(II)若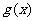 在其定义域内为单调函数,求
在其定义域内为单调函数,求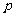 的取值范围;
的取值范围;
(III)证明:
① 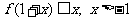 ;
;
② 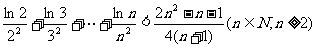 .
.
(13)若点P(3,1)是圆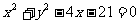 的弦AB的中点,则直线AB的方程是 .
的弦AB的中点,则直线AB的方程是 .
(14)在代数式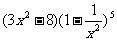 的展开式中,常数项的是
.
的展开式中,常数项的是
.
(15)在样本的频率分布直方图中,共有4个小长方形,这4个小长方形的面积由小到大构成等差数列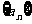 ,已知
,已知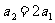 ,且样本容量为400,则小长方形面积最大的一组的频数为
.
,且样本容量为400,则小长方形面积最大的一组的频数为
.
(16)对于函数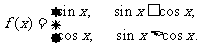 给出下列四个命题:
给出下列四个命题:
① 该函数是以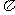 为最小正周期的周期函数;
为最小正周期的周期函数;
② 当且仅当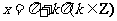 时,该函数取得最小值是-1;
时,该函数取得最小值是-1;
③ 该函数的图象关于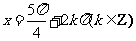 对称;
对称;
④当且仅当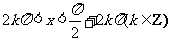 时,
时,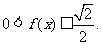
其中正确命题的序号是 (请将所有正确命题的序号都添上)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com