
10.若点P
( cos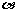 , sin
, sin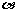 )在直线y = –2x上,则sin2
)在直线y = –2x上,则sin2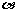 +2cos2
+2cos2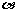 = ______________ 。
= ______________ 。
9.复数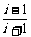 (i为虚数单位)的虚部是____________。
(i为虚数单位)的虚部是____________。
7.已知两个非零向量a = ( m –1 , n –1 )和b = ( m –3 , n –3 ),且a、b的夹角是钝角或直角,则m + n 的取值范围是( )
|
|
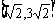 B.(2,6) C.
B.(2,6) C.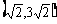 D.(2,6)
D.(2,6)
|
|
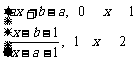 (其中b>0),若
(其中b>0),若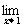 f ( x )存在,且f ( x )在(0,2)上有最大值,则b的取值范围是( )
f ( x )存在,且f ( x )在(0,2)上有最大值,则b的取值范围是( )
A.(1,+∞) B. C.
C.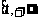 D.
D.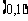
第Ⅱ卷(非选择题 共110分)
6.如图所球,正方体ABCD-A1B1C1D1,E、F分别是正方ADD1A1和ABCD的中心,G是CC1的中点,设GF、C1E与AB所成的角分别为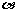 、
、 ,则
,则 +
+ 等于( )
等于( )
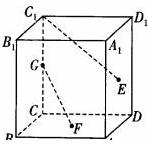
A.120° B.60° C.75° D.90°
5.椭圆满分这样的光党性质:从椭圆焦点发射光线,经椭圆反射后,反射孔液光线经过椭圆的另一个焦点。现在设有一个水平放置的椭圆形台球盘,满足方程: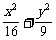 =1,点A,B是它的两个焦点,当静止的小球放在点A处,从点A沿直线出发,经椭圆壁反弹后,再回到点A时,小球经过的路程是( )
=1,点A,B是它的两个焦点,当静止的小球放在点A处,从点A沿直线出发,经椭圆壁反弹后,再回到点A时,小球经过的路程是( )
A.20 B.18 C.16 D.以上均有可能
4.设a1 = 2,数列{1 + 2an}是公比为2的等比数列,则a6 =( )
A.31.5 B.160 C.79.5 D.159.5
3.设p,q是简单命题,则“p且q为真”是“p或q为真”的( )
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.既不充分也不必要条件
|
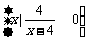 ,集合N=
,集合N=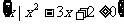 ,则集合
,则集合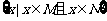 为( )
为( )
A.{x|x≥0} B.{x|x>0}
C.{x|x≥4或x≤0} D.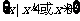
2. 已知函数y = f ( x )的反函数f –1( x ) = log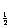
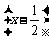 ,则方程f ( x ) = 1的解集是( )
,则方程f ( x ) = 1的解集是( )
A.{2} B.{1} C.{3} D.{4}
20.(本小题满分14分)
已知抛物线的顶点在原点,对称轴为y轴,且准线方程为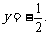 直线l过M(1,0)与抛物线交于A,B两点,点P在y轴的右侧且满足
直线l过M(1,0)与抛物线交于A,B两点,点P在y轴的右侧且满足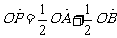 (O为坐标原点)。
(O为坐标原点)。
(Ⅰ)求抛物线的方程及动点P的轨迹方程;
(Ⅱ)记动点P的轨迹为C,若曲线C的切线斜率为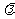 ,满足
,满足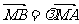 ,点A到y轴的距离为a,求a的取值范围。
,点A到y轴的距离为a,求a的取值范围。
19.(本小题满分14分)
|
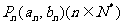 都在直线l:
都在直线l: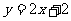 上,P1为直线l与x轴的交点,数列
上,P1为直线l与x轴的交点,数列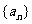 成等差数列,公差为1。
成等差数列,公差为1。
(Ⅰ)求数列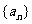 ,
,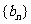 的通项公式;
的通项公式;
(Ⅱ)若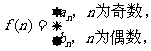 问是否存在
问是否存在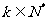 ,使得
,使得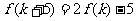 成立?若存在,求出k的值,若不存在,说明理由。
成立?若存在,求出k的值,若不存在,说明理由。
(Ⅲ)求证:
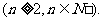
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com