
1.设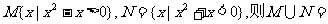 ( )
( )
A.R B.M C.N D.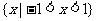
参考公式:
如果事件A、B互斥,那么
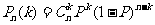
P(A+B)=P(A)+P(B)
球的表面积公式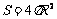
如果事件A、B相互独立,那么
P(A·B)=P(A)·P(B) 其中R表示球的半径
如果事件A在一次试验中发生的概率是
球的体积公式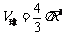
P,那么n次独立重复试验中恰好发生k次的概率 : 其中R表示球的半径
(17)(本小题满分12分)
命题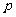 :方程
:方程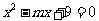 有两个不相等的负根;
有两个不相等的负根;
命题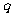 :方程
:方程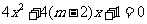 无实根.
无实根.
已知“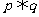 ”为真命题,“
”为真命题,“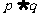 ”为假命题,求实数m的取值范围.
”为假命题,求实数m的取值范围.
(18)(本小题满分12分)
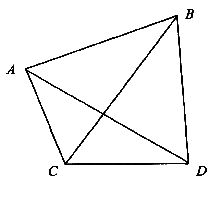
数学课外小组的同学想在岸上测出A、B两个海岛之间的距离,他们在岸边选取了相距约为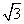 千米的C、D两点,测得∠ACB=75°,∠ADC=30°,∠BCD=45°,∠ADB=45°,假定A、B、C、D四点均在同一平面上,求A、B之间的距离.
千米的C、D两点,测得∠ACB=75°,∠ADC=30°,∠BCD=45°,∠ADB=45°,假定A、B、C、D四点均在同一平面上,求A、B之间的距离.
(19)(本小题满分12分)
解关于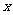 的不等式
的不等式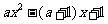 >
>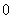 .
.
(20)(本小题满分12分)
已知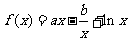 ,在
,在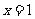 与
与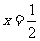 处都取得极值.
处都取得极值.
(I)求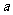 、
、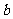 的值及
的值及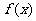 的解析式。
的解析式。
(Ⅱ)若对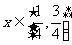 时,
时,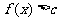 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(21)(本小题满分12分)
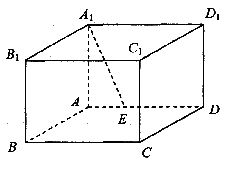
如图,长方体ABCD-AlB1ClD1中,AA1=AB=6,AD=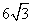 ,点E在棱AD上,且∠DEA1=120°
,点E在棱AD上,且∠DEA1=120°
(I)求异面直线A1E、ACl所成角的大小:
(II)求二面角Al-BD-C的大小:
(Ⅲ)求点A到平面AlBD的距离.
(22)(本小题满分14分)
已知椭圆Cl: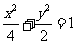 ,动直线
,动直线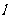 垂直于
垂直于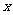 轴且与椭圆C1交于A、B两点,P是动直线
轴且与椭圆C1交于A、B两点,P是动直线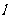 上一点,满足
上一点,满足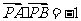
(Ⅰ)求点P的轨迹方程C2;
(Ⅱ)过点M(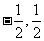 )的直线与C2相交于C、D两点,且点M恰为弦CD的中点,求直线CD的方程。
)的直线与C2相交于C、D两点,且点M恰为弦CD的中点,求直线CD的方程。
(Ⅲ)设(Ⅱ)中直线CD与椭圆Cl相交于E、F两点,求弦EF的长.
(13)直线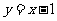 被抛物线
被抛物线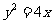 截得线段的中点坐标是_________
截得线段的中点坐标是_________
(14)若命题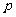 :
: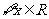 ,
,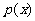 ≥0.则
≥0.则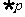 :___________
:___________
(15)已知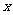 >
>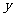 >0,
>0,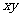 =1,则
=1,则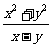 的最小值为__________
的最小值为__________
(16)已知函数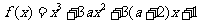 既有极大值又有极小值,则
既有极大值又有极小值,则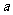 的取值范围是_______
的取值范围是_______
(1)不等式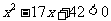 的解集是
的解集是
(A)[-14,-3] (B)(-14,-3) (C)[3,14] (D)(3,14)
(2)若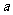 <
<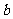 <
<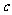 ,则
,则
(A)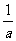 <
<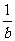 (B)
(B)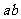 >
>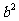 (C)
(C)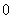 <
<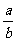 <
<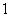 (D)
(D)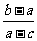 <
<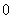
(3)下列四个命题
①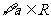 ,函数
,函数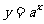 是单调函数; ②
是单调函数; ②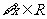
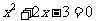 ;
;
③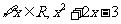 ≥
≥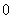 ; ④
; ④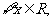 如果
如果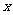 >
>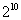 ,那么
,那么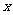 >
>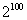 .
.
其中真命题的个数为
(A)0个 (B)1个 (C)2个 (D)3个
(4)抛物线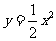 的焦点坐标是
的焦点坐标是
(A)(0,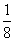 ) (B)(0,
) (B)(0,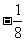 ) (C)(0,
) (C)(0,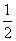 ) (D)(0,
) (D)(0,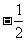 )
)
(5)平面的一条斜线和这个平面所成角θ的范围是
(A)0°<θ<90° (B)0°≤θ<90°
(C)0°<θ≤90° (D)0°<θ<180°
(6)过椭圆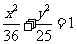 的一个焦点
的一个焦点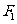 作直线交椭圆于A、B两点,
作直线交椭圆于A、B两点,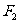 是椭圆的另一个焦点,则△
是椭圆的另一个焦点,则△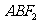 的周长是
的周长是
(A)12 (B)24 (C)22 (D)10
(7)曲线 在点(1,-1)处的切线方程为
在点(1,-1)处的切线方程为
(A)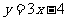 (B)
(B)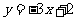
(C)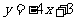 (D)
(D)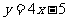
(8)双曲线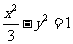 的离心率是
的离心率是
(A)3 (B)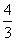 (C)
(C)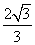 (D)
(D) 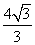
(9)若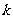 为整数,且满足P(3,一1),Q(2,一4)两点分别处在直线
为整数,且满足P(3,一1),Q(2,一4)两点分别处在直线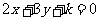 的相反两侧,则满足条件的
的相反两侧,则满足条件的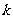 的值的总和为
的值的总和为
(A)0
(B)25 (C)-3<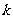 <8
(D)-22
<8
(D)-22
(10)已知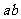 ≠0,那么
≠0,那么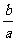 >l是
>l是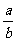 <1的
<1的
(A)充分条件但不是必要条件
(B)必要条件但不是充分要件
(C)充要条件
(D)既不充分也不必要条件
(11)在△ABC中,a=4, b=3,a与b的夹角为60°,则△ABC的第三边c等于
(A)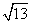 (B)
(B)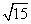 (C)
(C)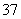 (D)
(D)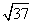
(12)空间四边形ABCD的每条边和对角线的长都等于4,点E、F分别是BC、AD的中点,则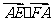 的值为
的值为
(A)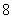 (B)
(B)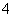 (C)
(C)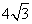 (D)
(D)
第Ⅱ卷(非选择题共90分)
21、(本大题满分14分)已知定义域为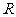 的函数
的函数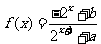 是奇函数。
是奇函数。
(Ⅰ)求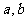 的值;
的值;
(Ⅱ)若对任意的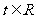 ,不等式
,不等式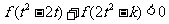 恒成立,求
恒成立,求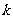 的取值范围;
的取值范围;
20、(本题满分16分)已知函数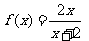 ,定义数列
,定义数列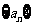 ,使:
,使: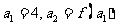 ,…,
,…,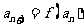 … .
… .
(1)求证:数列{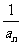 }是等差数列;
}是等差数列;
(2)设数列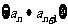 的前n项和为Sn,求证:Sn <8.
的前n项和为Sn,求证:Sn <8.
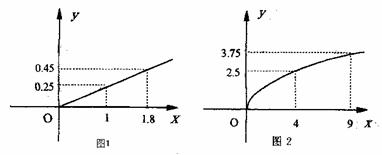
19、(本大题满分16分)某民营企业生产A、B两种产品,根据市场调查与预测,A产品的利润与投资成正比,其关系如图1,B产品的利润与投资的算术平方根成正比,其关系如图2(注:利润与投资单位:万元)(1)分别写出将A、B两种产品的利润表示为投资的函数关系式
(2)该企业已筹集到10万元资金,并全部投入A、B两种产品的生产,问:怎样分配这10万元投资,才能使企业获得最大利润,其最大利润约为多少万元(精确到1万元)
18、(本小题满分12分)设等差数列{an}的首项a1及公差d都为整数,前n项和为Sn.
(1)若a11=0,S14=98,求数列{an}的通项公式;
(2)若a1≥6,a11>0,S14≤77,求所有可能的数列{an}的通项公式.
17、(本小题满分12分)二次函数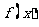 满足
满足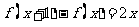 ,且
,且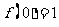 .
.
(1) 求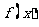 的解析式;
的解析式;
(2) 在区间[-1,1]上,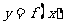 的图象恒在
的图象恒在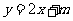 的图象上方,试确定实数m的取值范围.
的图象上方,试确定实数m的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com