
4. 函数 的反函数是( )
的反函数是( )
A. B.
B.
C.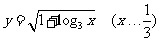 D.
D.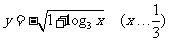
3. 设a,b∈R则“lg (a2+1)<lg (b2+1)”是a<b的
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
2. 已知复数 满足
满足 ,那么复数
,那么复数 的虚部为( )
的虚部为( )
A. 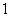 B.
B.
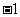 C.
C.
 D.
D.

1. 设全集U=R,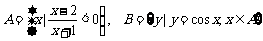 ,则
,则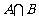 =( )
=( )
A.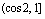 B.
B.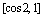 C.
C.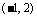 D.
D.
20.(本小题14分)
设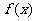 是定义在R上的偶函数,且对于任意
是定义在R上的偶函数,且对于任意 都有
都有 。且在区间
。且在区间 上,
上, 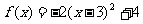 。
。
(1)求 的值;
的值;
(2)求出曲线 在点
在点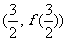 处的切线方程;
处的切线方程;
(3)若矩形ABCD的两顶点A、B在 轴上,两顶点C、D在函数
轴上,两顶点C、D在函数 的图象上,求这个矩形面积的最大值。
的图象上,求这个矩形面积的最大值。
19.(本小题14分)
已知数列 的前
的前 项和为
项和为 ,
, 的前
的前 项和为
项和为 ,且
,且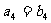 。
。
(1)求数列 、
、 的通项公式;
的通项公式;
(2)若对于数列 有,
有,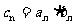 ,请求出数列
,请求出数列 的前n项和
的前n项和
18.(本小题14分)
已知椭圆的对称中心在坐标原点,对称轴为坐标轴,其中一个焦点的坐标为 。椭圆与y轴交于A、B两点,其中点A的坐标为
。椭圆与y轴交于A、B两点,其中点A的坐标为
(1)求此椭圆的方程;
(2)若点C在该椭圆上,且|CF1|=4,请求此时△ABC的面积。
17.(本小题14分)
已知函数 求:
求:
(1)函数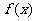 的最小正周期;
的最小正周期;
(2)函数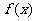 的最大值和最小值;
的最大值和最小值;
(3)函数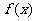 的单调递增区间。
的单调递增区间。
16.(本小题12分)
 如图,直三棱柱
如图,直三棱柱 中,∠A’C’B’=90°,侧面A’ACC’为正方形,D、E分别为AB、B’C’的中点。
中,∠A’C’B’=90°,侧面A’ACC’为正方形,D、E分别为AB、B’C’的中点。
(1)求证:A’C⊥平面AB’C’;
(2)求证:DE∥平面ACC’ A’。
15.(本小题12分)
甲、乙、丙三人进行射击比赛,他们独自射击命中目标的概率分别为 、
、 、
、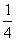 。现三人同时对同一目标进行射击,求目标被击中的概率。
。现三人同时对同一目标进行射击,求目标被击中的概率。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com