
(1)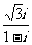 的共轭复数是
的共轭复数是
(A)
-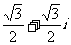 (B)
(B)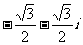 (C)
(C)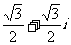 (D)
(D)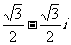
(2)已知条件P: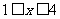 ,条件
,条件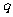 :
: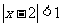 ,则
,则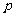 是
是
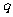 的
的
 (A)充分不必要条件 (B)必要不充分条件
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既非充分也非必要条件
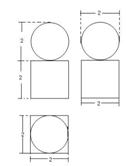
(3)一个几何体的三视图如图所示,则该几何体的体积等于
(A)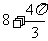 (B)
(B) 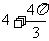
(C)  (D)
(D) 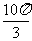
(4)设某种动物由出生算起活到10岁的概率为0.9,活到15岁的概率为0.6.现有一个10岁的这种动物,它能活到15岁的概率是
(A)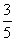 (B)
(B)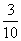 (C)
(C)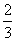 (D)
(D)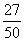
(5)设F是椭圆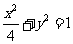 的右焦点,椭圆上的点与点F的最大距离为M,最小距离是m,则椭圆上与点F的距离是
的右焦点,椭圆上的点与点F的最大距离为M,最小距离是m,则椭圆上与点F的距离是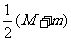 的点的坐标是
的点的坐标是
(A) (0,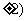 (B)
(B)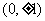 (C)
(C)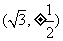 (D)
(D) 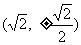
 (6)已知
(6)已知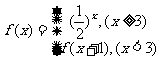 , 则
, 则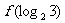 的值是
的值是
(A)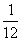 (B)
(B)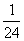 (C)
24
(D) 12
(C)
24
(D) 12
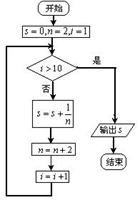
(7)如图,程序框图所进行的求和运算是
(A)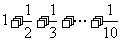
(B)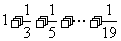
(C)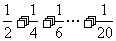
(D)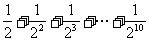
(8)设双曲线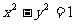 的两条渐近线与直线
的两条渐近线与直线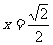 围成的三角形区域(包含边界)为D, P(
围成的三角形区域(包含边界)为D, P(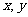 )为D内的一个动点,则目标函数
)为D内的一个动点,则目标函数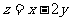 的最小值为
的最小值为
(A)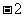 (B)
(B)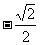 (C)0 (D)
(C)0 (D)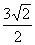
(9)设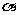 、
、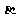 、
、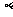 为平面,
为平面,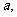
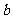 为直线,给出下列条件
为直线,给出下列条件
① 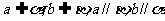 ;
;
② 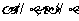 ;
;
③ 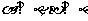 ;
;
④ 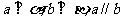
其中能使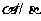 成立的条件是
成立的条件是
(A)①② (B) ②③ (C) ② ④ (D) ③④
(10) 已知幂函数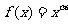 的部分对应值如下表:
的部分对应值如下表:
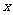 |
1 |
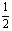 |
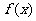 |
1 |
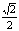 |
则不等式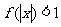 的解集是
的解集是
(A)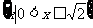 (B)
(B)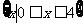 (C)
(C)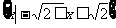 (D)
(D) 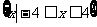
(11)在股票买卖过程中,经常用到两种曲线,一种是即时价格曲线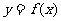 ,另一种是平均价格曲线
,另一种是平均价格曲线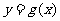 (如f(2)=3是价格开始买卖后2小时的即时价格为3元;g(2)=3表示2小时内的平均价格为3元),下面给出了四个图象,其中实线表示y=f(x),虚线表示y=g(x),其中可能正确的是
(如f(2)=3是价格开始买卖后2小时的即时价格为3元;g(2)=3表示2小时内的平均价格为3元),下面给出了四个图象,其中实线表示y=f(x),虚线表示y=g(x),其中可能正确的是
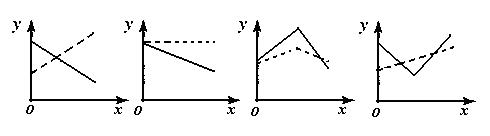
(A) (B) (C) (D)
(12)已知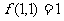 ,
,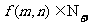 (
(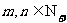 )且对任意
)且对任意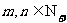 都有
都有
① 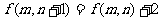 ;
;
② 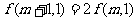 .
.
则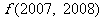 的值为
的值为
(A)  (B)
(B) (C)
(C) (D)
(D)
(17)(本小题满分12分)
已知数列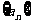 是各项均为正数的等比数列,且
是各项均为正数的等比数列,且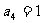 ,
,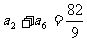 .
.
求数列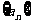 的通项公式.
的通项公式.
(18)(本小题满分12分)
在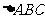 中,已知角
中,已知角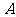 为锐角,且
为锐角,且

(Ⅰ)求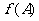 的最大值;
的最大值;
(Ⅱ)若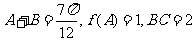 ,求
,求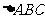 的三个内角和
的三个内角和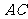 边的长.
边的长.
(19)(本小题满分12分)
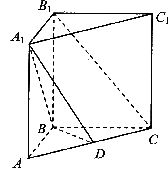 如图所示,在直三棱柱
如图所示,在直三棱柱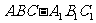 中,
中,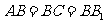 ,
,
D为AC的中点.
(Ⅰ)求证: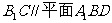
(Ⅱ)若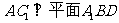 ,求证:
,求证: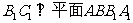 ;
;
(Ⅲ)在(Ⅱ)的条件下, AB=1,求三棱锥B-A1C1D的体积.
(20)(本小题满分12分)
某工厂每天生产某种产品最多不超过40件,并且在生产过程中产品的正品率P与每日生产量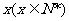 件间的关系为
件间的关系为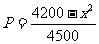 ,每生产一件正品盈利4000元,每出现一件次品亏损2000元.(注:正品率=产品中的正品件数÷产品总件数×100%)
,每生产一件正品盈利4000元,每出现一件次品亏损2000元.(注:正品率=产品中的正品件数÷产品总件数×100%)
(Ⅰ)将日利润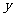 (元)表示成日产量
(元)表示成日产量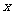 (件)的函数;
(件)的函数;
(Ⅱ)求该厂的日产量为多少件时,日利润最大?并求出日利润的最大值.
(21)(本小题满分12分)
已知函数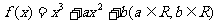 .
.
(Ⅰ)若 ,且
,且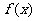 的极大值为5,极小值为1,求
的极大值为5,极小值为1,求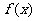 的解析式;
的解析式;
(Ⅱ)若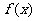 在
在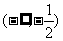 上是增函数,求
上是增函数,求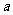 的取值范围.
的取值范围.
(22)(本小题满分14分)
已知椭圆C的焦点在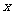 轴上,一个顶点的坐标是
轴上,一个顶点的坐标是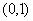 ,离心率等于
,离心率等于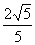 .
.
(Ⅰ)求椭圆C的方程。
(Ⅱ)过椭圆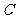 的右焦点F作直线
的右焦点F作直线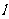 ,交椭圆C于A、B两点,交
,交椭圆C于A、B两点,交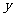 轴于
轴于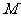 点,若
点,若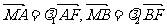 ,求证
,求证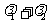 为定值.
为定值.
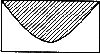 (13)已知右图所示的矩形,其长为12,宽为5.在矩形内随机
(13)已知右图所示的矩形,其长为12,宽为5.在矩形内随机
地撒1000颗黄豆,数得落在阴影部分的黄豆数为550颗.
则可以估计出阴影部分的面积约为 _____________.
(14)抛物线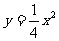 的焦点坐标是____________.
的焦点坐标是____________.
(15)已知6名同学中恰有两名女同学,从这6名同学中任选两人参加某项活动,则在选出的同学中至少包括一名女同学的概率是_________ .
(16)数列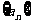 的前
的前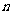 项和
项和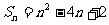 ,则
,则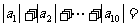 __________.
__________.
(1)复数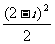 (
(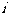 是虚数单位)等于
是虚数单位)等于
(A) (B)
(B)  (C)
(C) 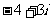 (D)
(D) 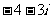
(2)老师在班级50名学生中,依次抽取学号为5,10,15,20,25,30,35,40,45,50的学生进行作业检查,这种抽样方法是
(A)随机抽样 (B)分层抽样 (C)系统抽样 (D)以上都不是
(3)设双曲线的焦点在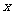 轴上,两条渐近线为
轴上,两条渐近线为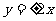 ,则该双曲线的离心率为
,则该双曲线的离心率为
 (A)
(A) 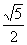 (B)
(B)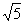 (C)
(C) 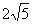 (D)
(D)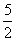
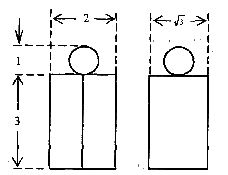
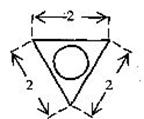
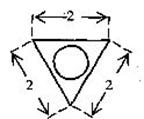
(4)右图为一个几何体的三视图,尺寸如图所示,
则该几何体的体积为
(A)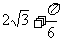 (B)
(B) 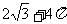
(C) 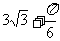 (D)
(D) 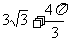
 (5)已知圆C与圆
(5)已知圆C与圆 关于直线
关于直线
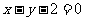 对称,则圆C的方程是
对称,则圆C的方程是
(A)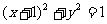
(B) 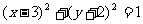
(C) 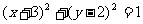
(D) 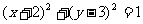
(6)不等式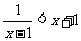 的解集是
的解集是
(A) (B)
(B)

(C) 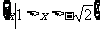 (D)
(D)
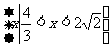
(7) 已知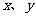 满足约束条件
满足约束条件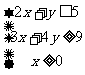 ,则
,则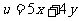 的最小值是
的最小值是
(A)9
(B)20 (C)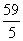 (D)
(D) 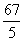
(8) 已知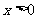 ,
,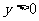 ,
,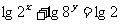 ,则
,则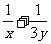 的最小值是
的最小值是
(A)2 (B)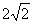 (C)4
(D)
(C)4
(D) 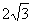
(9)在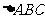 中,D是BC边的中点,E是AD的中点,若
中,D是BC边的中点,E是AD的中点,若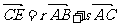 ,则
,则 的值是
的值是
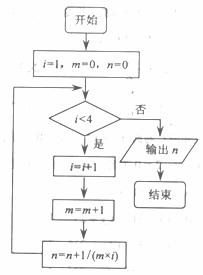 (A)1 (B)
(A)1 (B)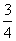 (C)
(C) 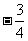 (D)
(D) 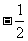
(10) 右图是一个算法的程序框图, 该算法所输出的结果是
(A) 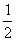
(B) 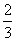
(C) 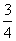
(D) 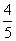
(11)已知球的表面积等于16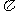 ,圆台上、下底面圆周都在球面上,且下底面过球心,圆台的轴截面的底角为
,圆台上、下底面圆周都在球面上,且下底面过球心,圆台的轴截面的底角为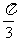 ,则圆台的轴截面的面积是
,则圆台的轴截面的面积是
(A)9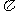 (B)
(B)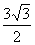 (C)
(C) 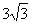 (D)6
(D)6
(12)已知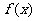 是定义在
是定义在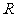 上的偶函数,则“
上的偶函数,则“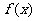 是周期函数”的一个充要条件是
是周期函数”的一个充要条件是
(A)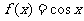 (B)
(B) 
(C) 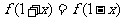 (D)
(D) 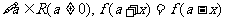
第Ⅱ卷(非选择题共90分)
(17)(本小题满分12分)
在 中,已知角
中,已知角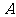 为锐角,且
为锐角,且
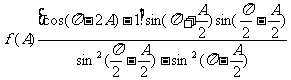
(Ⅰ)求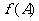 的最大值;
的最大值;
(Ⅱ)若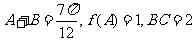 ,求
,求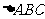 的三个内角和
的三个内角和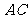 边的长.
边的长.
(18)(本小题满分12分)
某单位有8名员工,其中有5名员工曾经参加过一种或几种技能培训,另外3名员工没有参加过任何技能培训.现要从8名员工中任选3人参加一种新的技能培训.
(Ⅰ)求恰好选到1名曾经参加过技能培训的员工的概率;
(Ⅱ)这次培训结束后,仍然没有参加过任何技能培训的员工人数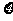 是一个随机变量,求
是一个随机变量,求 的分布列和数学期望.
的分布列和数学期望.
 (19)(本小题满分12分)
(19)(本小题满分12分)
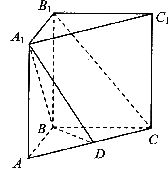
如图所示,在直三棱柱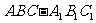 中,
中,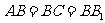 ,
,
D为AC的中点.
(Ⅰ)求证: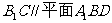
(Ⅱ)若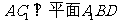 ,求证:
,求证: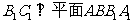 ;
;
(Ⅲ)在(Ⅱ)的条件下, 求二面角B-A1C1-D的大小.
(20)(本小题满分12分)
已知椭圆C的焦点在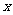 轴上,它的一个顶点恰好是抛物线
轴上,它的一个顶点恰好是抛物线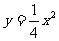 的焦点,离心率等于
的焦点,离心率等于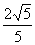 .
.
(Ⅰ)求椭圆C的方程。
(Ⅱ)过椭圆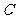 的右焦点F作直线
的右焦点F作直线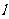 ,交椭圆C于A、B两点,交
,交椭圆C于A、B两点,交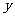 轴于
轴于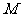 点,若
点,若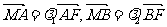 ,求证
,求证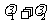 为定值.
为定值.
(21)(本小题满分12分)
已知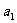 ,
,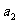 ,…,
,…,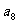 是首项为1,公比为2 的等比数列,对于
是首项为1,公比为2 的等比数列,对于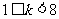 的整数
的整数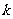 ,数列
,数列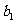 ,
,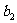 ,…,
,…,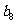 由
由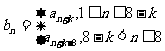 确定,记
确定,记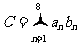 .
.
(Ⅰ)求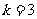 时
时 的值(求出具体的数值);
的值(求出具体的数值);
(Ⅱ)求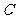 最小时
最小时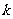 的值.
的值.
(22)(本小题满分14分)
已知函数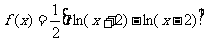 ,且
,且 恒成立.
恒成立.
(Ⅰ)求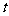 的值
的值
(Ⅱ)求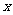 为何值时,
为何值时,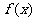 在
在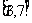 上取得最大值;
上取得最大值;
(Ⅲ) 设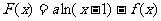 ,若
,若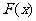 是单调递增函数,求
是单调递增函数,求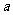 的取值范围.
的取值范围.
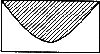 (13)已知右图所示的矩形,其长为12,宽为5.在矩形内随机
(13)已知右图所示的矩形,其长为12,宽为5.在矩形内随机
地撒1000颗黄豆,数得落在阴影部分的黄豆数为550颗.
则可以估计出阴影部分的面积约为 _____________.
(14)定积分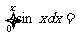 ____________.
____________.
(15) 数列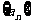 的前
的前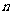 项和
项和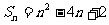 ,则
,则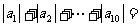 __________.
__________.
(16)已知在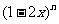 的展开式中,各项的二项式系数之和是64,则
的展开式中,各项的二项式系数之和是64,则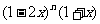 的展开式中,
的展开式中,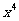 项的系数是_________ .
项的系数是_________ .
(1)复数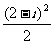 (
(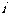 是虚数单位)等于
是虚数单位)等于
(A) (B)
(B)  (C)
(C) 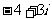 (D)
(D) 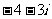
(2)老师在班级50名学生中,依次抽取学号为5,10,15,20,25,30,35,40,45,50的学生进行作业检查,这种抽样方法是
(A)随机抽样 (B)分层抽样 (C)系统抽样 (D)以上都不是
(3)设双曲线的焦点在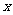 轴上,两条渐近线为
轴上,两条渐近线为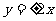 ,则该双曲线的离心率为
,则该双曲线的离心率为
(A)
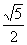 (B)
(B)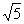 (C)
(C) 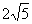 (D)
(D)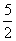
(4)右图为一个几何体的三视图,尺寸如图所示,则该几何体的体积为
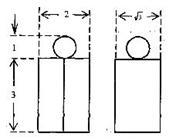 (A)
(A)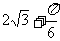 (B)
(B) 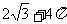
(C) 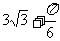 (D)
(D) 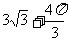
 (5)已知圆C与圆
(5)已知圆C与圆 关于直线
关于直线
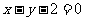 对称,则圆C的方程是
对称,则圆C的方程是
(A)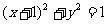
(B) 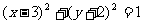
(C) 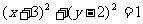
(D) 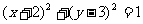
(6)不等式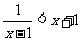 的解集是
的解集是
(A) 
(B) 
(C) 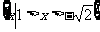
(D) 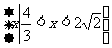
(7) 已知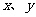 满足约束条件
满足约束条件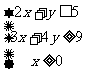 ,则
,则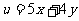 的最小值是
的最小值是
(A)9 (B)20 (C)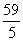 (D)
(D) 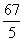
(8) 已知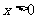 ,
,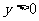 ,
,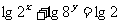 ,则
,则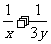 的最小值是
的最小值是
(A)2
(B)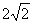 (C)4
(D)
(C)4
(D) 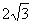
(9)要得到函数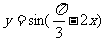 的图象,只需将函数
的图象,只需将函数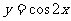 的图像
的图像
(A)向右平移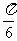 个单位 (B) 向右平移
个单位 (B) 向右平移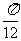 个单位
个单位
(C)向左平移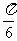 个单位 (D) 向左平移
个单位 (D) 向左平移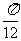 个单位
个单位
(10) 右图是一个算法的程序框图,该算法所输出的结果是
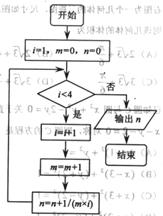 (A)
(A) 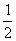
(B) 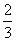
(C) 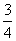
(D) 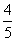
(11)已知球的表面积等于16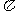 ,圆台上、下底面圆周都在球面上,且下底面过球心,圆台的轴截面的底角为
,圆台上、下底面圆周都在球面上,且下底面过球心,圆台的轴截面的底角为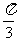 ,则圆台的轴截面的面积是
,则圆台的轴截面的面积是
(A)9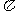 (B)
(B)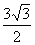 (C)
(C) 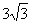 (D)6
(D)6
(12)已知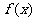 是定义在
是定义在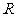 上的偶函数,则“
上的偶函数,则“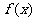 是周期函数”的一个充要条件是
是周期函数”的一个充要条件是
(A)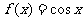 (B)
(B) 
(C) 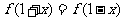 (D)
(D) 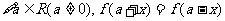
第Ⅱ卷(非选择题共90分)
22.(本小题满分14分)
设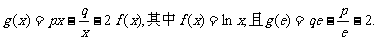 (e为自然对数的底数)
(e为自然对数的底数)
(Ⅰ)求p与q的关系;
(Ⅱ)若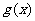 在其定义域内为单调函数,求p的取值范围;
在其定义域内为单调函数,求p的取值范围;
(Ⅲ)证明:
①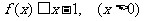 ;
;
②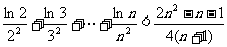 (n∈N,n≥2).
(n∈N,n≥2).
21.(本小题满分12分)
已知中心在原点,焦点在x轴上的椭圆,离心率e=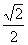 ,且经过抛物线x2=4y的焦点.
,且经过抛物线x2=4y的焦点.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)若过点B(2,0)的直线l(斜率不等于零)与椭圆交于不同的两点E、F(E在B、F之间),试求△OBE与△OBF面积之比的取值范围.
20. (本小题满分12分)
(本小题满分12分)
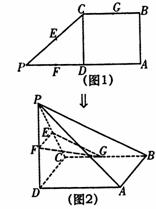
如图1,在直角梯形ABCP中,AP∥BC,AP⊥AB,
AB=BC=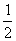 AP=2,D为AP的中点,E,F,G分别为PC、
AP=2,D为AP的中点,E,F,G分别为PC、
PD、CB的中点,将△PCD沿CD折起,使点P在平面
ABCD内的射影为点D,如图2.
(Ⅰ)求证:AP∥平面EFG;
(Ⅱ)求三棱锥P-ABC的体积.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com