
5.已知直线l:y=x+2,椭圆C: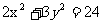 ,设l与C的交点为A,B,并用
,设l与C的交点为A,B,并用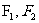 表示椭圆C的左、右焦点,则△ABF2的周长为
表示椭圆C的左、右焦点,则△ABF2的周长为
(A)16 (B) 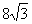 (C)12 (D)
(C)12 (D) 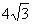
4.在△ABC中,a、b、c表示三边长,A、B、C表示三个内角的大小,设命题p: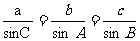 ,命题q:a=b=c.那么命题p是命题q成立的
,命题q:a=b=c.那么命题p是命题q成立的
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分又不必要条件
3.直线l与平面的夹角为40°,则直线l与平面α内的任意直线的夹角中最大、最小的角分别是
(A)90°,40° (B)140°,40° (C)140°,0° (D)90°,0°
2.已知定点F1(1,2),F2(一5,10),动点M满足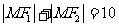 ,则动点M的轨迹为
,则动点M的轨迹为
(A)线段 (B)椭圆 (C)双曲线 (D)抛物线
1.给出下列命题:
①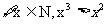 ;
;
②如果直线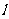 ⊥平面
⊥平面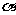 ,
,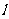 ∥平面
∥平面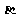 ,那么
,那么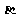 ⊥
⊥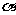 ;
;
③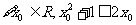 ;
;
④存在一个空间四边形,它的对角线互相垂直.
其中真命题的个数是
(A) 0 (B) 1 (C) 2 (D) 3
21.(本小题满分12分)
如图,圆C的半径为定长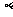 ,A是圆C外的一个定点,P是圆C上的任意一点,线段AP的垂直平分线
,A是圆C外的一个定点,P是圆C上的任意一点,线段AP的垂直平分线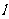 和半径CP所在直线相交于点Q.
和半径CP所在直线相交于点Q.
(1)当点P在圆上运动时,试判断点Q的轨迹类型,并说明理由;
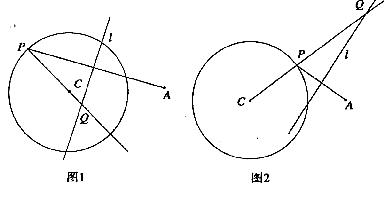
第21(1)题图
(2)如果设圆C的方程为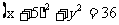 ,点A的坐标为(5,0),求点Q的轨迹方程.
,点A的坐标为(5,0),求点Q的轨迹方程.
20.(本小题满分12分)
甲、乙两物体分别从相距70m的两处同时相向运动,甲第一分钟走2m,以后每分钟比前l分钟多走1m,乙每分钟走5m.
(1)甲、乙开始运动后几分钟相遇?
(2)如果甲、乙到达对方起点后立即折返,甲继续每分钟比前1分钟多走1m,乙继续每分钟走5m,那么开始运动几分钟后第二次相遇?
19.(本小题满分l2分)
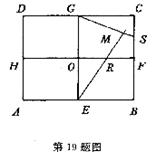 如图,在矩形ABCD中,
如图,在矩形ABCD中,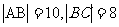 ,E,F,G,H分别是矩形四条边的中点,点R在线段OF上,点S在线段CF上,且
,E,F,G,H分别是矩形四条边的中点,点R在线段OF上,点S在线段CF上,且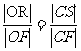 ,直线ER与直线GS相交于点M,试证明点M在以HF为长轴、以EG为短轴的椭圆上.
,直线ER与直线GS相交于点M,试证明点M在以HF为长轴、以EG为短轴的椭圆上.
18.(本小题满分10分)
函数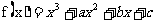 ,过曲线
,过曲线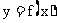 上的点P(1,f(1))的切线方程为y=3x+1.
上的点P(1,f(1))的切线方程为y=3x+1.
(1)若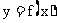 在
在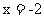 时有极值,求
时有极值,求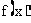 的表达式;
的表达式;
(2)在(1)的条件下,求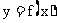 在[一3,1]上的最大值.
在[一3,1]上的最大值.
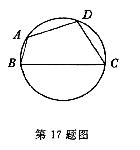
17.(本小题满分10分)
已知圆内接四边形ABCD的边长分别为AB=2,BC=6,CD=DA=4,求四边形ABCD的面积.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com