
2.数形结合,以形助数是解决本节问题常用的思想方法.
1.函数的奇偶性经常与函数的其他性质,如单调性、周期性、对称性结合起来考查.因此,在复习过程中应加强知识横向间的联系.
2.有时可直接根据图象的对称性来判断函数的奇偶性.
●教师下载中心
教学点睛
1.函数的奇偶性是函数的整体性质,即自变量x在整个定义域内任意取值.
8.设f(x)=log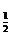 (
(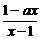 )为奇函数,a为常数,
)为奇函数,a为常数,
(1)求a的值;
(2)证明f(x)在(1,+∞)内单调递增;
(3)若对于[3,4]上的每一个x的值,不等式f(x)>(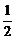 )x+m恒成立,求实数m的取值范围.
)x+m恒成立,求实数m的取值范围.
(1)解:f(x)是奇函数,∴f(-x)=-f(x).
∴log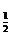
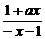 =-log
=-log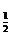
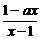
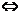
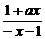 =
=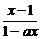 >0
>0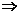 1-a2x2=1-x2
1-a2x2=1-x2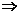 a=±1.检验a=1(舍),∴a=-1.
a=±1.检验a=1(舍),∴a=-1.
(2)证明:任取x1>x2>1,∴x1-1>x2-1>0.
∴0<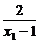 <
<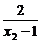
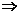 0<1+
0<1+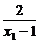 <1+
<1+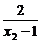
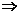 0<
0<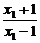 <
<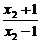
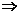 log
log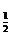
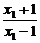 >log
>log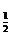
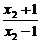 ,即f(x1)>f(x2).∴f(x)在(1,+∞)内单调递增.
,即f(x1)>f(x2).∴f(x)在(1,+∞)内单调递增.
(3)解:f(x)-(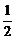 )x>m恒成立.
)x>m恒成立.
令g(x)=f(x)-(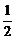 )x.只需g(x)min>m,用定义可以证g(x)在[3,4]上是增函数,∴g(x)min=g(3)=-
)x.只需g(x)min>m,用定义可以证g(x)在[3,4]上是增函数,∴g(x)min=g(3)=-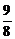 .∴m<-
.∴m<-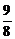 时原式恒成立.
时原式恒成立.
●思悟小结
7.已知f(x)=x(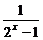 +
+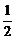 ).
).
(1)判断f(x)的奇偶性;
(2)证明f(x)>0.
(1)解:f(x)=x·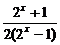 ,其定义域为x≠0的实数.又f(-x)=-x·
,其定义域为x≠0的实数.又f(-x)=-x·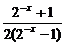 =-x·
=-x·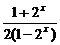 =x·
=x·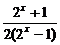 =f(x),
=f(x),
∴f(x)为偶函数.
(2)证明:由解析式易见,当x>0时,有f(x)>0.
又f(x)是偶函数,且当x<0时-x>0,
∴当x<0时f(x)=f(-x)>0,
即对于x≠0的任何实数x,均有f(x)>0.
探究创新
6.(理)定义在[-2,2]上的偶函数g(x),当x≥0时,g(x)单调递减,若g(1-m)<g(m),求m的取值范围.
解:由g(1-m)<g(m)及g(x)为偶函数,可得g(|1-m|)<g(|m|).又g(x)在(0,+∞)上单调递减,∴|1-m|>|m|,且|1-m|≤2,|m|≤2,解得-1≤m<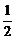 .
.
说明:也可以作出g(x)的示意图,结合图形进行分析.
(文)(2005年北京西城区模拟题)定义在R上的奇函数f(x)在(0,+∞)上是增函数,又f(-3)=0,则不等式xf(x)<0的解集为
A.(-3,0)∪(0,3) B.(-∞,-3)∪(3,+∞)
C.(-3,0)∪(3,+∞) D.(-∞,-3)∪(0,3)
解析:由奇偶性和单调性的关系结合图象来解.
答案:A
培养能力
5.若f(x)=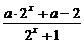 为奇函数,求实数a的值.
为奇函数,求实数a的值.
解:∵x∈R,∴要使f(x)为奇函数,必须且只需f(x)+f(-x)=0,即a-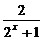 +
+
a-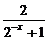 =0,得a=1.
=0,得a=1.
4.(2003年北京)函数f(x)=lg(1+x2),g(x)=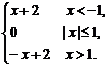 h(x)=tan2x中,______________是偶函数.
h(x)=tan2x中,______________是偶函数.
解析:∵f(-x)=lg[1+(-x)2]=lg(1+x2)=f(x),
∴f(x)为偶函数.
又∵1°当-1≤x≤1时,-1≤-x≤1,
∴g(-x)=0.
又g(x)=0,∴g(-x)=g(x).
2°当x<-1时,-x>1,
∴g(-x)=-(-x)+2=x+2.
又∵g(x)=x+2,∴g(-x)=g(x).
3°当x>1时, -x<-1,
∴g(-x)=(-x)+2=-x+2.
又∵g(x)=-x+2,∴g(-x)=g(x).
综上,对任意x∈R都有g(-x)=g(x).
∴g(x)为偶函数.
h(-x)=tan(-2x)=-tan2x=-h(x),
∴h(x)为奇函数.
答案:f(x)、g(x)
3.已知f(x)是奇函数,当x∈(0,1)时,f(x)=lg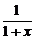 ,那么当x∈(-1,0)时,f(x)的表达式是__________.
,那么当x∈(-1,0)时,f(x)的表达式是__________.
解析:当x∈(-1,0)时,-x∈(0,1),∴f(x)=-f(-x)=-lg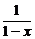 =lg(1-x).
=lg(1-x).
答案:lg(1-x)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com