2.用导数求多项式函数单调区间的一般步骤.

(1)求(x).

(2)(x)>0的解集与定义域的交集的对应区间为增区间；

(x)<0的解集与定义域的交集的对应区间为减区间.

●点击双基

1.利用导数研究多项式函数单调性的一般步骤.

(1)求(x).

(2)确定(x)在(a，b)内符号.

(3)若(x)>0在(a，b)上恒成立，则f(x)在(a，b)上是增函数；

若(x)<0在(a，b)上恒成立，则f(x)在(a，b)上是减函数.

13.2　 导数的应用

●知识梳理

3.可以用单调性求函数的极值、最值.

●教师下载中心

教学点睛

利用导数解有关函数的单调性、极值、最值的问题是本节的主要题型，也是高考考查的重点，复习时应引起足够的重视.解单调性的题目时要注意判断端点能否取到，用导数求单调函数的最值时要注意由极值到最值的过渡.

拓展题例

[例题] 设函数y=f(x)=ax³+bx²+cx+d图象与y轴的交点为P,且曲线在P点处的切线方程为24x+y－12=0,若函数在x=2处取得极值－16,试求函数解析式,并确定函数的单调递减区间.

错因点评：有的同学不知道P点处的斜率为y′|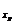,即y′|_x=0为已知切线方程的斜率　 －24.又当x=2时有极值,且极值为－16,找不到与a、b、c、d的关系,从而无法求出a、b、c、d,导致错解.

正确思路：由y′=3ax²+2bx+c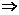f′(0)=c,

∵切线24x+y－12=0的斜率k=－24,

∴c=－24,把x=0代入24x+y－12=0得y=12.

得P点的坐标为(0,12),由此得d=12,f(x)即可写成f(x)=ax³+bx²－24x+12.

由函数f(x)在x=2处取得极值－16,则得

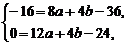解得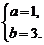

∴f(x)=x³+3x²－24x+12,f′(x)=3x²+6x－24.令f′(x)＜0,得－4＜x＜2.

∴递减区间为(－4,2).

2.函数单调性的必要条件，设f(x)在(a,b)内可导，若f(x)在(a,b)上单调递增(或递减)，则f′(x)≥0(或f′(x)≤0)且f′(x)在(a,b)的任意子区间上都不恒为零.

1.函数单调性的充分条件，若f′(x)＞0(或＜0)，则f(x)为增函数(或减函数).

9.已知函数f(x)的图象与函数h(x)=x+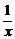+2的图象关于点A(0，1)对称.

(1)求f(x)的解析式；

(2)若g(x)=f(x)+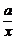,且g(x)在区间(0，2］上为减函数，求实数a的取值范围.

解:(1)设f(x)图象上任一点坐标为(x,y)，点(x,y)关于点A(0，1)的对称点(－x,2－y)在h(x)图象上.

∴2－y=－x+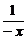+2.

∴y=x+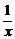,即f(x)=x+.

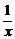(2)g(x)=x+ ,

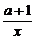∵g′(x)=1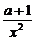－,g(x)在(0，2］上递减，

∴1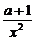－≤0在x∈(0,2］时恒成立,

即a≥x²－1在x∈(0,2)时恒成立.

∵x∈(0,2]时，(x²－1) _max=3,∴a≥3.

●思悟小结

8.(2004年全国Ⅱ，文21)若函数f(x)=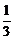x³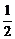－ax²+(a－1)x+1在区间(1,4)内为减函数，在区间(6，+∞)上为增函数，试求实数a的取值范围.

解:函数f(x)的导数f′(x)=x²－ax+a－1.

令f′(x)=0,解得x=1或x=a－1.

当a－1≤1，即a≤2时，函数f(x)在(1,+∞)上为增函数，不合题意.

当a－1＞1,即a＞2时，函数f(x)在(－∞,1)上为增函数，在(1,a－1)内为减函数，在(a－1,+∞)上为增函数.

依题意应有

当x∈(1,4)时，f′(x)＜0,

当x∈(6,+∞)时，f′(x)＞0.

所以4≤a－1≤6,解得5≤a≤7.

所以a的取值范围是［5,7］.

探究创新

7.已知x∈R,求证：e^x≥x+1.

证明:设f(x)=e^x－x－1,则f′(x)=e^x－1.

∴当x=0时，f′(x)=0,f(x)=0.

当x＞0时，f′(x)＞0,∴f(x)在(0,+∞)上是增函数.∴f(x)＞f(0)=0.

当x＜0时，f′(x)＜0,f(x)在(－∞,0)上是减函数，∴f(x)＞f(0)=0.

∴对x∈R都有f(x)≥0.∴e^x≥x+1.

6.(2004年全国Ⅰ,理19)已知a∈R，求函数f(x)=x²e^ax的单调区间.

解:f′(x)=2xe^ax+ax²e^ax=(2x+ax²)e^ax.

①当a=0时，若x＜0，则f′(x)＜0，若x＞0,则f′(x)＞0.

所以当a=0时，函数f(x)在区间(－∞,0)内为减函数，在区间(0，+∞)内为增　　　　　 函数.

②当a＞0时，由2x+ax²＞0，解得x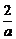＜－或x＞0;由2x+ax²＜0,得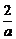－＜x＜0.

所以当a＞0时，函数f(x)在区间(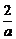－∞，－)内为增函数，在区间(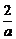－,0)内为减函数，在区间(0，+∞)内为增函数.

③当a＜0时，由2x+ax²＞0，得0＜x＜－.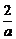

由2x+ax²＜0，得x＜0或x＞－.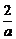

所以当a＜0时，函数f(x)在区间(－∞,0)内为减函数，在区间(0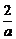，－)内为增函数，在区间(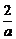－,+∞)内为减函数.

培养能力