5.(2005年北京西城区抽样测试题)已知命题p:函数y=log_a(ax+2a)(a＞0且a≠1)的图象必过定点(－1，1)；

命题q:如果函数y=f(x－3)的图象关于原点对称，那么函数y=f(x)的图象关于点(3，0)对称.则

A.“p且q”为真　　　　　　　　　　　　　　　　　　　　　　 B.“p或q”为假

C. p真q假　　　　　　　　　　　　　　　　　　　　　　　　　　 D. p假q真

解析：解决本题的关键是判定p、q的真假.由于p真，q假(可举反例y=x+3)，因此正确答案为C.

答案：C

●典例剖析

[例1] 给出命题“已知a、b、c、d是实数，若a=b，c=d，则a+c=b+d”，对其原命题、逆命题、否命题、逆否命题而言，真命题有

A.0个　　　　　　　　　　　　　 B.2个　　　　　　　　　　　　　 C.3个　　　　　　　　　　　　　 D.4个

剖析：原命题和逆否命题为真.

答案：B

深化拓展

若a、b、c∈R，写出命题“若ac＜0，则ax²+bx+c=0有两个不相等的实数根”的逆命题、否命题、逆否命题，并判断这三个命题的真假.

思路：认清命题的条件p和结论q，然后按定义写出逆命题、否命题、逆否命题，最后判断真假.

解：逆命题“若ax²+bx+c=0(a、b、c∈R)有两个不相等的实数根，则ac＜0”是假命题，如当a=1，b=－3，c=2时，方程x²－3x+2=0有两个不等实根x₁=1，x₂=2，但ac=2＞0.

否命题“若ac≥0，则方程ax²+bx+c=0(a、b、c∈R)没有两个不相等的实数根”是假命题.这是因为它和逆命题互为逆否命题，而逆命题是假命题.

逆否命题“若ax²+bx+c=0(a、b、c∈R)没有两个不相等的实数根，则ac≥0”是真命题.因为原命题是真命题，它与原命题等价.

评述：解答命题问题，识别命题的条件p与结论q的构成是关键.

[例2] 指出下列复合命题的形式及其构成.

(1)若α是一个三角形的最小内角，则α不大于60°；

(2)一个内角为90°，另一个内角为45°的三角形是等腰直角三角形；

(3)有一个内角为60°的三角形是正三角形或直角三角形.

解：(1)是非p形式的复合命题，其中p:若α是一个三角形的最小内角，则α＞60°.

(2)是p且q形式的复合命题，其中p:一个内角为90°，另一个内角为45°的三角形是等腰三角形，q:一个内角为90°，另一个内角为45°的三角形是直角三角形.

(3)是p或q形式的复合命题，其中p:有一个内角为60°的三角形是正三角形，q：有一个内角为60°的三角形是直角三角形.

[例3] 写出命题“当abc=0时，a=0或b=0或c=0”的逆命题、否命题、逆否命题，并判断它们的真假.

剖析：把原命题改造成“若p则q”形式，再分别写出其相应的逆命题、否命题、逆否命题.在判断真假时要注意利用等价命题的原理和规律.

解：原命题：若abc=0，则a=0或b=0或c=0，是真命题.

逆命题：若a=0或b=0或c=0，则abc=0，是真命题.

否命题：若abc≠0，则a≠0且b≠0且c≠0，是真命题.

逆否命题：若a≠0且b≠0且c≠0，则abc≠0，是真命题.

●闯关训练

夯实基础

4.命题“若m＞0，则关于x的方程x²+x－m=0有实数根”与它的逆命题、否命题、逆否命题中，真命题的个数为___________________.

解析：先写出其命题的逆命题、否命题、逆否命题，逐一判断.

答案：2

3.(2005年春季上海，15)设函数f(x)的定义域为R，有下列三个命题：

①若存在常数M，使得对任意x∈R，有f(x)≤M，则M是函数f(x)的最大值；

②若存在x₀∈R，使得对任意x∈R，且x≠x₀，有f(x)＜f(x₀)，则f(x₀)是函数f(x)的最大值；

③若存在x₀∈R，使得对任意x∈R，有f(x)≤f(x₀)，则f(x₀)是函数f(x)的最大值.

这些命题中，真命题的个数是

A.0　　 　　　　　　　　　　　 B.1 　　　　　　　　　　　　　 C.2　　 　　　　　　　　　　　 D.3

解析：①错.原因：可能“=”不能取到.②③都正确.

答案：C

2.(2004年福建，3)命题p:若a、b∈R，则|a|+|b|＞1是|a+b|＞1的充分而不必要条件；

命题q:函数y=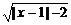的定义域是(－∞，－1］∪［3，+∞)，则

A.“p或q”为假　　　　　　　　　　　　　　　　　　　　　　 B.“p且q”为真

C. p真q假　　　　　　　　　　　　　　　　　　　　　　　　　　 D. p假q真

解析：∵|a+b|≤|a|+|b|，

若|a|+|b|＞1，不能推出|a+b|＞1，而|a+b|＞1，一定有|a|+|b|＞1，故命题p为假.

又由函数y=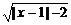的定义域为|x－1|－2≥0，即|x－1|≥2，即x－1≥2或x－1≤－2.

故有x∈(－∞，－1］∪［3，+∞).

∴q为真命题.

答案：D

1.由“p:8+7=16，q:π＞3”构成的复合命题，下列判断正确的是

A.p或q为真，p且q为假，非p为真

B.p或q为假，p且q为假，非p为真

C.p或q为真，p且q为假，非p为假

D.p或q为假，p且q为真，非p为真

解析：因为p假，q真，由复合命题的真值表可以判断，p或q为真，p且q为假，非p为真.

答案：A

2.四种命题

(1)四种命题

原命题：如果p，那么q(或若p则q)；逆命题：若q则p；

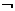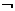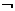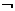否命题：若p则q；逆否命题：若q则p.

(2)四种命题之间的相互关系

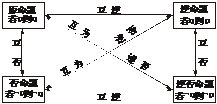
这里，原命题与逆否命题，逆命题与否命题是等价命题.

●点击双基

1.逻辑联结词

(1)命题：可以判断真假的语句叫做命题.

(2)逻辑联结词：“或”“且”“非”这些词叫做逻辑联结词.

(3)简单命题与复合命题：不含逻辑联结词的命题叫简单命题；由简单命题和逻辑联结词构成的命题叫做复合命题.

(4)真值表：表示命题真假的表叫真值表.

1.2　 逻辑联结词与四种命题

●知识梳理

3.强化数形结合、分类讨论的数学思想.

拓展题例

[例1] 设M、N是两个非空集合，定义M与N的差集为M－N={x|x∈M且x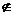N}，则M－(M－N)等于

A.N　　　　　　　　　　　　　　 B.M∩N　　　　　　　　　　　 C.M∪N　　　　　　　　　　　 D.M

解析：M－N={x|x∈M且x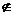N}是指图(1)中的阴影部分.

同样M－(M－N)是指图(2)中的阴影部分.

答案：B

[例2] 设集合P={1，a，b}，Q={1，a²，b²}，已知P=Q，求1+a²+b²的值.

解：∵P=Q，

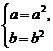∴　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　 ①

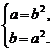或　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　 ②

解①得a=0或a=1，b=0或b=1.(舍去)

由②得a=b²=a⁴，∴a=1或a³=1.

a=1不合题意，

∴a³=1(a≠1).

∴a=ω，b=ω²，其中ω=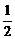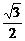－+i.

故1+a²+b²=1+ω²+ω⁴=1+ω+ω²=0.

2.集合问题多与函数、方程、不等式有关，要注意各类知识的融会贯通.