1.排列的概念：从n个不同元素中任取m个元素，按照一定的次序排成一列，叫做从n个不同元素中取出m个元素的一个排列.排列的个数叫做从n个不同元素中取出m个元素的排列数，用A表示.

10.2　 排列

●知识梳理

2.元素能重复的问题往往用计数原理.

●教师下载中心

教学点睛

弄清两个原理的区别与联系，是正确使用这两个原理的前提和条件.这两个原理都是指完成一件事而言的.其区别在于：(1)分类计数原理是“分类”，分步计数原理是“分步”；(2)分类计数原理中每类办法中的每一种方法都能独立完成一件事，分步计数原理中每步中每种方法都只能做这件事的一步，不能独立完成这件事.

拓展题例

[例1] 关于正整数2160，求：

(1)它有多少个不同的正因数？

(2)它的所有正因数的和是多少？

解：(1)∵N=2160=2⁴×3³×5，

∴2160的正因数为P=2^α×3^β×5^γ，

其中α=0，1，2，3，4，β=0，1，2，3，γ=0，1.

∴2160的正因数共有5×4×2=40个.

(2)式子(2⁰+2¹+2²+2³+2⁴)×(3⁰+3¹+3²+3³)×(5⁰+5¹)的展开式就是40个正因数.

∴正因数之和为31×40×6=7440.

[例2] 球台上有4个黄球，6个红球，击黄球入袋记2分，击红球入袋记1分，欲将此十球中的4球击入袋中，但总分不低于5分，击球方法有几种？

解：设击入黄球x个，红球y个符合要求，

则有　 x+y=4，

2x+y≥5(x、y∈N)，得1≤x≤4.

∴

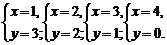
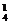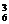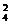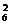相应每组解(x，y)，击球方法数分别为CC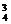，CC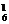，CC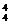，CC.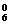

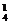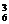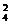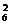共有不同击球方法数为CC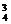+CC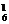+CC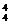+CC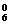=195.

1.分类计数原理和分步计数原理是解决排列、组合问题的理论基础.这两个原理的本质区别在于分类与分步，分类用分类计数原理，分步用分步计数原理.

10.三边长均为整数，且最大边长为11的三角形的个数是多少?

解：设较小的两边长为x、y且x≤y，

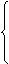则　 x≤y≤11，

x+y>11，

x、y∈N^*.

当x=1时，y=11；

当x=2时，y=10，11；

当x=3时，y=9，10，11；

当x=4时，y=8，9，10，11；

当x=5时，y=7，8，9，10，11；

当x=6时，y=6，7，8，9，10，11；

当x=7时，y=7，8，9，10，11；

……

当x=11时，y=11.

所以不同三角形的个数为

1+2+3+4+5+6+5+4+3+2+1=36.

评述：本题关键是列出约束条件，然后寻找x=1，2，…，11时，y的取值个数的规律，再用分类计数原理求解.

●思悟小结

9.五名学生报名参加四项体育比赛，每人限报一项，报名方法的种数为多少？又他们争夺这四项比赛的冠军，获得冠军的可能性有多少种？

解：(1)5名学生中任一名均可报其中的任一项，因此每个学生都有4种报名方法，5名学生都报了项目才能算完成这一事件.故报名方法种数为4×4×4×4×4=4⁵种.

(2)每个项目只有一个冠军，每一名学生都可能获得其中的一项获军，因此每个项目获冠军的可能性有5种.故有n=5×5×5×5=5⁴种.

探究创新

8.(理)设有编号为1，2，3，4，5的五个球和编号为1，2，3，4，5的五个盒子.现将这五个球投放入这五个盒子内，要求每个盒子内投放一球，并且恰好有两个球的编号与盒子的编号相同，则这样的投放方法有多少种?

分析：五个球分别投放到五个盒子内，恰好有两个球的编号与盒子的编号相同，则其他三个球必不能投放到与球的编号相同的盒子内，此时，这三个球与对应的三个盒子，就成了受限的特殊元素与特殊位置.

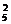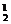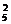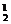解：先在五个球中任选两个球投放到与球编号相同的盒子内，有C种；剩下的三个球，不失一般性，不妨设编号为3，4，5，投放3号球的方法数为C，则投放4，5号球的方法只有一种，根据分步计数原理共有C·C=20种.

评述：本题投放球有两种方法，一种是投入到与编号相同的盒子内，另一种是投入到与编号不同的盒子内，故应分步完成.

(文)在所有两位数中，个位数字大于十位数字的两位数共有多少个?

分析：在0~9这10个数字中，按照题目要求组成的两位数中，个位数字不能为0和1，十位数字不能为0和9.也就是说组成两位数的数字可按个位分类或按十位分类来计算.

解法一：按个位数字是2，3，4，5，6，7，8，9分成8类，在每一类中满足条件的两位数分别是1个，2个，3个，4个，5个，6个，7个，8个.

则共有1+2+3+4+…+7+8=36(个).

解法二：按十位数字是1，2，3，4，5，6，7，8分成8类，在每一类中满足条件的两位数分别是8个，7个，6个，5个，4个，3个，2个，1个.

则共有8+7+6+5+4+3+2+1=36(个).

评述：在具体分类或分步时，常遇到困难，要多练习，多积累经验，掌握思维方法，逐步做到恰当分类，合理分步.

7.(2003年全国)如图，一个地区分为5个行政区域，现给地图着色，要求相邻区域不得使用同一颜色.现有4种颜色可供选择，则不同的着色方法共有_____________种.(以数字作答)

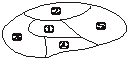
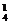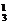解析：依次染①、②、③、④、⑤.故有C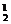·C·C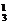·C·C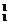=72种.

答案：72

6.(2001年上海)某餐厅供应客饭，每位顾客可以在餐厅提供的菜肴中任选2菜2素共4种不同的品种.现在餐厅准备了5种不同的荤菜，若要保证每位顾客有200种以上的不同选择，则餐厅至少还需要不同的素菜品种_____________种.(结果用数值表示)

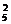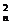解析：设素菜n种，则C·C≥200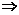n(n－1)≥40，所以n的最小值为7.

答案：7

培养能力

5.4棵柳树和4棵杨树栽成一行，柳树、杨树逐一相间的栽法有_____________种.

解析：2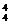A·A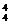=1152种.

答案：1152