
3.对于选择题的答案要谨慎选择,注意等价答案的不同形式.处理这类选择题可从分析答案形式入手,采用排除法.错误的答案,都是犯有重复或遗漏的错误.
●教师下载中心
教学点睛
2.对于较难直接解决的问题则可用间接法,但应做到不重不漏.
1.解排列、组合混合题一般是先选元素、后排元素,或充分利用元素的性质进行分类、分步,再利用两个基本原理作最后处理.
8.有点难度哟!
6名运动员分到4所学校去做教练,每校至少1人,有多少种不同的分配方法?
分析:人员分配有两类:1,1,1,3或1,1,2,2.
解法一:先取人,后取位子.
1,1,1,3:6人中先取3人有C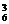 种取法,与剩余3人分到4所学校去有A
种取法,与剩余3人分到4所学校去有A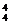 种不同分法,∴共C
种不同分法,∴共C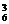 A
A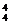 种分法;
种分法;
1,1,2,2:6人中取2人、2人、1人、1人的取法有C ·C
·C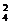 ·C
·C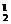 种,然后分到4所学校去,有
种,然后分到4所学校去,有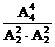 种不同的分法,共C
种不同的分法,共C ·C
·C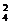 ·C
·C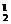 ·
·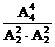 种分法.所以符合条件的分配方法有C
种分法.所以符合条件的分配方法有C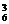 A
A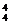 +C
+C ·C
·C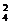 ·C
·C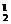 ·
·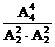 =1560种.
=1560种.
解法二:先取位子,后取人.
1,1,1,3:取一个位子放3个人,有C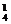 种取法,6人中分别取3人、1人、1人、1人的取法有C
种取法,6人中分别取3人、1人、1人、1人的取法有C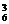 ·C
·C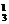 ·C
·C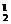 ·C
·C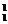 种,∴共有C
种,∴共有C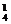 ·C
·C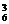 ·C
·C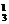 ·C
·C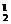 ·C
·C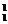 种.
种.
1,1,2,2:先取2个位子放2(其余2个位子放1)有C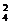 种取法,6人中分别取2人,2人,1人,1人的取法有C
种取法,6人中分别取2人,2人,1人,1人的取法有C ·C
·C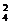 ·C
·C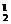 ·C
·C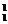 种,共有C
种,共有C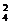 ·C
·C ·C
·C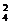 ·C
·C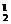 ·C
·C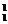 种.
种.
所以符合条件的分配方法有C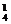 ·C
·C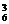 ·C
·C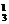 ·C
·C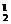 +C
+C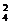 ·C
·C ·C
·C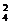 ·C
·C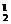 =1560种.
=1560种.
●思悟小结
7.(理)如下图,矩形的对角线把矩形分成A、B、C、D四部分,现用五种不同色彩给四部分涂色,每部分涂1种颜色,要求共边的两部分颜色互异,共有多少种不同的涂色方法?
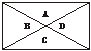
解法一:依题意,给四部分涂色,至少要用两种颜色,故可分成三类涂色:
第一类,用4种颜色涂色,有A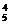 种方法;
种方法;
第二类,用3种颜色涂色,选3种颜色的方法有C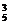 种;在涂的过程中,选对顶的两部分(A、C或B、D)涂同色,另两部分涂异色有C
种;在涂的过程中,选对顶的两部分(A、C或B、D)涂同色,另两部分涂异色有C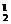 种选法;3种颜色涂上去有A
种选法;3种颜色涂上去有A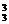 种涂法.共C
种涂法.共C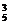 ·C
·C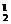 ·A
·A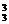 种涂法;
种涂法;
第三类,用两种颜色涂色.选颜色有C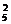 种选法;A、C与B、D各涂一色有A
种选法;A、C与B、D各涂一色有A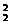 种涂法.共C
种涂法.共C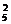 ·A
·A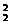 种涂法.
种涂法.
所以共有涂色方法A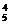 +C
+C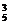 ·C
·C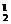 ·A
·A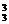 +C
+C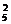 ·A
·A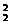 =260种.
=260种.
解法二:区域A有5种涂色法;区域B有4种涂色法;区域C的涂色法有2类:若C与A涂同色,区域D有4种涂色法;若C与A涂不同色,此时区域C有3种涂色法,区域D也有3种涂色法.
所以共有5×4×4+5×4×3×3=260种涂色法.
(文)10只不同的试验产品,其中有4只次品,6只正品,现每次取一只测试,直到4只次品全测完为止.求第4只次品正好在第五次测试时被发现的不同情形有多少种?
分析:这个问题实际上可以看成是有约束条件的“10选5”排列.主要约束条件是第5个位置上的限定.考查对这类问题的“10选5”模型的转化.
解:优先考虑第五次(位置)测试.这五次测试必有一次是测试正品,有C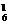 种;4只次品必有一只排在第五次测试,有A
种;4只次品必有一只排在第五次测试,有A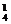 种;那么其余3只次品和一只正品将在第1至第4次测试中实现,有A
种;那么其余3只次品和一只正品将在第1至第4次测试中实现,有A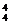 种.于是根据分步计数原理有C
种.于是根据分步计数原理有C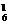 A
A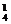 A
A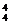 种.
种.
评述:C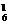 A
A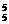 是本题的错解,原因是这样排正好有可能正品出现在第五次测试.
是本题的错解,原因是这样排正好有可能正品出现在第五次测试.
探究创新
6.18人的旅游团要选一男一女参加生活服务工作,有两位老年男人不在推选之列,共有64种不同选法,问这个团中男女各几人?
解:设这个团中有男人x人,则有女人18-x人,根据题意得C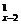 · C
· C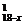 =64.解得x=10.
=64.解得x=10.
∴这个团中有男10人,女8人.
5.在一张节目表上原有6个节目,如果保持这些节目的相对顺序不变,再添加进去三个节目,求共有多少种安排方法?
解法一:添加的三个节目有三类办法排进去:①三个节目连排,有C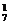 A
A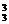 种方法;②三个节目互不相邻,有A
种方法;②三个节目互不相邻,有A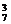 种方法;③有且仅有两个节目连排,有C
种方法;③有且仅有两个节目连排,有C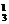 C
C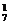 C
C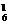 A
A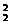 种方法.根据分类计数原理共有C
种方法.根据分类计数原理共有C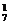 A
A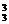 +A
+A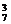 +C
+C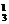 C
C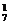 C
C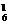 A
A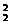 =504种.
=504种.
解法二:从结果考虑,排好的节目表中有9个位置,先排入三个添加节目有A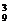 种方法,余下的六个位置上按6个节目的原有顺序排入只有一种方法.故所求排法为A
种方法,余下的六个位置上按6个节目的原有顺序排入只有一种方法.故所求排法为A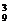 =504种.
=504种.
解法三: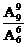 =504.
=504.
评述:插空法是处理排列、组合问题常用的方法.
培养能力
4.(2004年浙江,文16)设坐标平面内有一个质点从原点出发,沿x轴跳动,每次向正方向或负方向跳1个单位,经过5次跳动质点落在点(3,0)(允许重复过此点)处,则质点不同的运动方法共有__________种.(用数字作答)
解析:记向左跳一次为-1,向右跳一次为+1,则只要5次和为+3,质点一定落在(3,0),
所以只需4个“+1”,1个“-1”即可,从5次中挑出一次取“-1”,结果数为C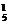 =5,故质点运动方法共有5种.
=5,故质点运动方法共有5种.
答案:5
3.书架上原有5本书,再放上2本,但要求原有书的相对顺序不变,则不同的放法有_____________种.
解析:分三步,每步各有6,7,8种放法,共有6×7×8=336种.
答案:336
2.四个不同的小球全部随意放入三个不同的盒子中,使每个盒子都不空的放法种数为
A.A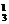 A
A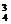 B.C
B.C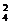 A
A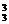 C.C
C.C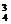 A
A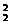 D.C
D.C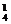 C
C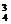 C
C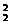
解析:4个球放入3个盒子,则有一个盒子要放两个球,故C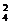 A
A .
.
答案:B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com