1.(2004年天津，理3)若平面向量b与向量a=(1，－2)的夹角是180°，且|b|=3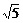，则b等于

A.(－3，6)　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.(3，－6)

C.(6，－3)　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.(－6，3)

解析：易知a与b方向相反，可设b=(λ，－2λ)(λ＜0).又|b|=3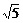=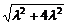，解之得λ=－3或λ=3(舍去).∴b=(－3，6).

答案：A

5.两个重要定理：

(1)向量共线定理：向量b与非零向量a共线的充要条件是有且仅有一个实数λ，使得b=λa，即b∥a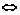b=λa(a≠0).

(2)平面向量基本定理：如果e₁、e₂是同一平面内的两个不共线向量，那么对于这一平面内的任一向量a，有且仅有一对实数λ₁、λ₂，使a=λ₁e₁+λ₂e₂.

●点击双基

4.实数与向量的积：

(1)定义：实数λ与向量a的积是一个向量，记作λa，规定：|λa|=|λ||a|.当λ＞0时，λa的方向与a的方向相同；当λ＜0时，λa的方向与a的方向相反；当λ=0时，λa与a平行.

(2)运算律：λ(μa)=(λμ)a，(λ+μ)a=λa+μa，λ(a+b)=λa+λb.

3.向量的减法：

(1)定义：求两个向量差的运算，叫做向量的减法.

(2)法则：三角形法则；平行四边形法则.

2.向量的加法：

(1)定义：求两个向量和的运算，叫做向量的加法.

(2)法则：三角形法则；平行四边形法则.

(3)运算律：a+b=b+a；(a+b)+c=a+(b+c).

1.平面向量的有关概念：

(1)向量的定义：既有大小又有方向的量叫做向量.

(2)表示方法：用有向线段来表示向量.有向线段的长度表示向量的大小，用箭头所指的方向表示向量的方向.用字母a，b，…或用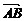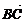，，…表示.

(3)模：向量的长度叫向量的模，记作|a|或||.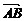

(4)零向量：长度为零的向量叫做零向量，记作0；零向量的方向不确定.

(5)单位向量：长度为1个长度单位的向量叫做单位向量.

(6)共线向量：方向相同或相反的向量叫共线向量，规定零向量与任何向量共线.

(7)相等的向量：长度相等且方向相同的向量叫相等的向量.

5.1　 向量的概念、向量的加法与减法、实数与向量的积

●知识梳理

4.了解平面向量基本定理，理解平面向量的坐标的概念，掌握平面向量的坐标运算.

●复习方略指南

向量是数学中的重要概念，它广泛应用于生产实践和科学研究中，其重要性逐渐加强.从近几年高考试题可以看出，主要考查平面向量的加减运算、平面向量的坐标表示、平面向量的数量积、图形的平移等基本概念、运算及简单应用.随着新教材的逐步推广、使用，“平面向量”将会成为命题的热点，一般选择题、填空题重在考查平面向量的概念、数量积及其运算律.本单元试题的常见类型有：

(1)与“定比分点”有关的试题；

(2)平面向量的加减法运算及其几何意义；

(3)平面向量的数量积及运算律，平面向量的坐标运算，用向量的知识解决几何问题；

(4)正、余弦定理的应用.

复习本章时要注意：

(1)向量具有大小和方向两个要素.用线段表示向量时，与有向线段起点的位置没有关系，同向且等长的有向线段都表示同一向量.

(2)共线向量和平面向量的两条基本定理，揭示了共线向量和平面向量的基本结构，它们是进一步研究向量的基础.

(3)向量的加、减、数乘积是向量的线性运算，其结果仍是向量.向量的数量积结果是一个实数.向量的数量积，可以计算向量的长度、平面内两点间距离、两个向量的夹角，判断相应的两条直线是否垂直.

(4)向量的运算与实数的运算有异同点，学习时要注意这一点，如数量积不满足结合律.

(5)要注意向量在几何、三角、物理学中的应用.

(6)平面向量与空间向量的数量积及坐标运算是高考的重点，复习中要注意培养准确的运算能力和灵活运用知识的能力.

3.掌握实数与向量的积的运算律及运算法则.

2.掌握向量的加法与减法的运算律及运算法则.