
1.|x|>a x>a或x<-a(a>0);
x>a或x<-a(a>0);
|x|<a -a<x<a(a>0).
-a<x<a(a>0).
6.5 不等式的解法(二)
●知识梳理
3.解不等式几乎是每年高考的必考题,重点仍是含参数的有关不等式,对字母参数的逻辑划分要具体问题具体分析,必须注意分类不重、不漏、完全、准确.
拓展题例
[例1] (2003年南京市第二次质量检测题)解关于x的不等式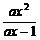 >x(a∈R).
>x(a∈R).
解法一:由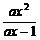 >x,得
>x,得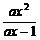 -x>0,即
-x>0,即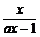 >0.
>0.
此不等式与x(ax-1)>0同解.
若a<0,则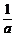 <x<0;
<x<0;
若a=0,则x<0;
若a>0,则x<0或x>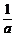 .
.
综上,a<0时,原不等式的解集是(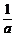 ,0);
,0);
a=0时,原不等式的解集是(-∞,0);
a>0时,原不等式的解集是(-∞,0)∪(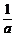 ,+∞).
,+∞).
解法二:由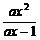 >x,得
>x,得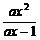 -x>0,即
-x>0,即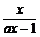 >0.
>0.
此不等式与x(ax-1)>0同解.
显然,x≠0.
(1)当x>0时,得ax-1>0.
若a<0,则x<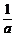 ,与x>0矛盾,
,与x>0矛盾,
∴此时不等式无解;
若a=0,则-1>0,此时不等式无解;
若a>0,则x>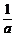 .
.
(2)当x<0时,得ax-1<0.
若a<0,则x>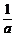 ,得
,得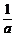 <x<0;
<x<0;
若a=0,则-1<0,得x<0;
若a>0,则x<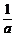 ,得x<0.
,得x<0.
综上,a<0时,原不等式的解集是(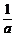 ,0);
,0);
a=0时,原不等式的解集是(-∞,0);
a>0时,原不等式的解集是(-∞,0)∪(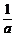 ,+∞).
,+∞).
[例2] f(x)是定义在(-∞,3]上的减函数,不等式f(a2-sinx)≤f(a+1+cos2x)对一切x∈R均成立,求实数a的取值范围.
解:由题意可得
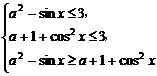
即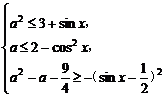 对x∈R恒成立.
对x∈R恒成立.
故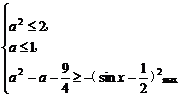
∴-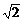 ≤a≤
≤a≤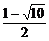 .
.
2.各类不等式最后一般都要化为一元一次不等式(组)或一元二次不等式(组)来解,这体现了转化与化归的数学思想.
1.解不等式的过程,实质上是不等式等价转化过程.因此在教学中向学生强调保持同解变形是解不等式应遵循的基本原则.
4.解含参数的不等式的基本途径是分类讨论,能避免讨论的应设法避免讨论.
●教师下载中心
教学点睛
3.解高次不等式的思路是降低次数,利用数轴标根法求解较为容易.
2.解分式不等式要使一边为零,转化为不等式组.如果能分解,可用数轴标根法或列表法.
1.一元二次不等式的解集与二次项系数及判别式的符号有关.
9.关于x的不等式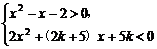 的整数解的集合为{-2},求实数k的取值范围.
的整数解的集合为{-2},求实数k的取值范围.
解:由x2-x-2>0可得x<-1或x>2.
∵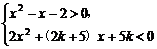 的整数解为x=-2,
的整数解为x=-2,
又∵方程2x2+(2k+5)x+5k=0的两根为-k和-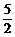 .
.
①若-k<-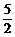 ,则不等式组的整数解集合就不可能为{-2};
,则不等式组的整数解集合就不可能为{-2};
②若-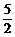 <-k,则应有-2<-k≤3.
<-k,则应有-2<-k≤3.
∴-3≤k<2.
综上,所求k的取值范围为-3≤k<2.
●思悟小结
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com