
题目列表(包括答案和解析)
7.一项研究要确定是否能够根据施肥量预测作物的产量。这里的预报变量是
A.作物的产量 B.施肥量
C.试验者 D.降雨量或其他解释产量的变量
6.若条件p: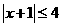 ,条件q:
,条件q: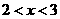 ,则
,则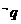 是
是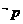 的
的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既非充分条件也非必要条件
5.下面几种推理过程为演绎推理的是
A.若两条直线平行,则同旁内角互补.如果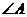 和
和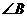 是两条平行直线的同旁内角,则
是两条平行直线的同旁内角,则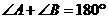 .
.
B.由平面三角形的性质,推测空间四面体的性质.
C.某校高三共有10个班,1班有51人,2班有53人,3班有52人,由此推测各班都超过50人.
D.在数列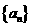 中,
中,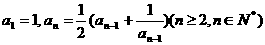 ,由此归纳出
,由此归纳出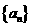 的通项公式.
的通项公式.
4.下列命题错误的是
A.命题“若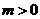 ,则方程
,则方程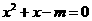 有实数根”的逆否命题为:“若方程
有实数根”的逆否命题为:“若方程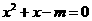 无实数根,则
无实数根,则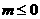 ”.
”.
B.“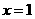 ”是“
”是“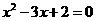 ”的充分不必要条件.
”的充分不必要条件.
C.若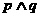 为假命题,则
为假命题,则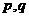 均为假命题.
均为假命题.
D.对于命题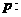
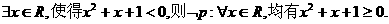
3.复数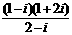 的值等于
的值等于
A.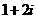 B.
B.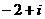 C.
C.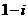 D.
D.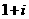
2.不等式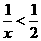 的解集是
的解集是
A.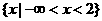 B.
B.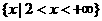
C.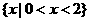 D.
D.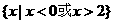
1.若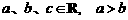 ,则下列不等式成立的是
,则下列不等式成立的是
A.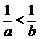 . B.
. B.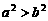 . C.
. C.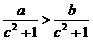 . D.
. D.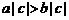 .
.
22.解: (I)由于函数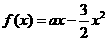 的最大值不小于
的最大值不小于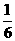 ,
,
所以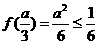 ,即
,即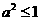 ①┅┅┅┅┅┅┅2分
①┅┅┅┅┅┅┅2分
又当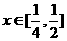 时,
时,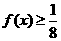 ,所以
,所以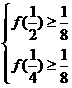 ,即
,即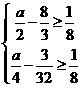 ,┅┅┅┅┅┅┅4分
,┅┅┅┅┅┅┅4分 

解得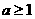 ②,由①②得
②,由①②得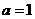 ┅┅┅┅┅┅┅5分
┅┅┅┅┅┅┅5分
(II) 证明:①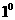 当
当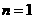 时, 由已知
时, 由已知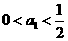 知不等式
知不等式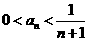 成立;因当
成立;因当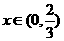 时
时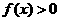 ,所以
,所以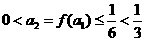 ,故
,故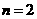 时不等式也成立.
时不等式也成立.
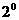 假设
假设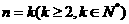 时,不等式
时,不等式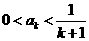 成立,因为函数
成立,因为函数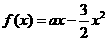 的对称轴为
的对称轴为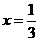 ,知
,知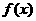 在
在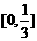 为增函数,所以由
为增函数,所以由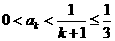 得
得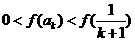 ,即
,即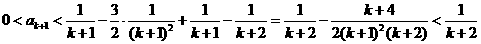 ,所以
,所以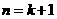 时,不等式也成立.根据
时,不等式也成立.根据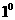
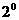 可知,对任意
可知,对任意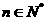 ,
,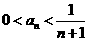 成立. ┅┅┅┅┅┅┅8分
成立. ┅┅┅┅┅┅┅8分
②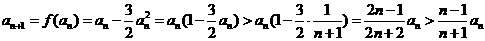 ,┅┅┅┅┅┅┅10分
,┅┅┅┅┅┅┅10分
从而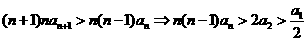 ┅┅┅┅┅┅┅12分
┅┅┅┅┅┅┅12分
当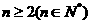 时
时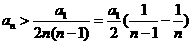 ,┅┅┅┅┅┅┅13分
,┅┅┅┅┅┅┅13分 

从而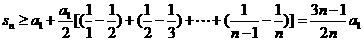 ┅┅┅┅┅┅┅14分
┅┅┅┅┅┅┅14分
21.解:(I)设第n年获取利润为y万元
n年共收入租金30n万元,付出装修费构成一个以1为首项,2为公差的等差数列,共
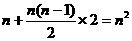 …………………………2分
…………………………2分
因此利润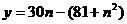 ,令
,令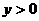 ……………………3分
……………………3分
解得: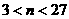 ,…………………………………….4分
,…………………………………….4分
所以从第4年开始获取纯利润 ………………………….5分
(II)纯利润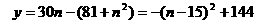
所以15后共获利润:144+ 10=154 (万元)………………………7分
年平均利润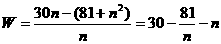
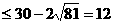 (当且仅当
(当且仅当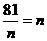 ,即n=9时取等号)
……..10分
,即n=9时取等号)
……..10分
所以9年后共获利润:12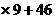 =154(万元)………………….11分
=154(万元)………………….11分
两种方案获利一样多,而方案②时间比较短,所以选择方案②……………12 分
20.解:(I)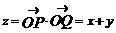 ┅┅┅┅┅┅┅2分
┅┅┅┅┅┅┅2分
易得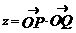 的最大值为6,最小值为2 ┅┅┅┅6分
的最大值为6,最小值为2 ┅┅┅┅6分
(II)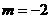 ┅┅┅┅┅┅┅12分
┅┅┅┅┅┅┅12分 

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com