
题目列表(包括答案和解析)
19.解(Ⅰ)设乙、丙两人各自通过测试的概率分别是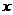 、
、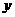 依题意得:
依题意得:

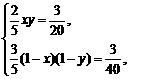 即
即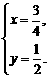 或
或 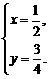 (舍去)┅┅┅┅┅┅┅4分
(舍去)┅┅┅┅┅┅┅4分
所以乙、丙两人各自通过测试的概率分别是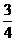 、
、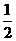 . ┅┅┅┅┅┅┅6分
. ┅┅┅┅┅┅┅6分
(Ⅱ)因为
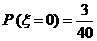
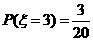
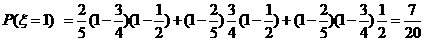


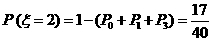
 所以
所以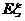 =
=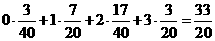 ┅┅┅┅┅┅┅12分
┅┅┅┅┅┅┅12分
(III)设甲,乙通过测试的事件分别为 A,B.则所求的事件的概率为
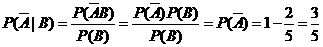
18.解: 由曲线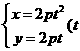 为参数,
为参数,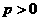 )消去参数得
)消去参数得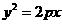 ,┅┅┅┅┅┅┅2分
,┅┅┅┅┅┅┅2分
已知直线参数方程为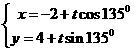 ┅┅┅┅┅┅┅4分
┅┅┅┅┅┅┅4分
代入曲线方程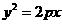 得
得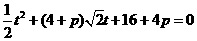 ,┅┅┅┅┅┅┅5分
,┅┅┅┅┅┅┅5分
设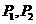 两点对应的参数分别为
两点对应的参数分别为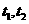 ,
,
则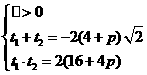 ,且
,且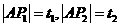 ┅┅┅┅┅┅┅6分
┅┅┅┅┅┅┅6分
又由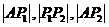 成等比数列知
成等比数列知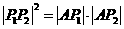 ,┅┅┅┅┅┅┅8分
,┅┅┅┅┅┅┅8分
即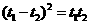 ,解得
,解得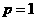 ┅┅┅┅┅┅┅10分
┅┅┅┅┅┅┅10分
17.解:(I)当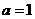 时,
时,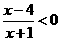 等价于
等价于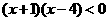 ,则解集
,则解集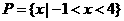 ┅┅4分
┅┅4分
(II)解法1:(1)当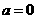 时,
时,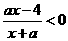 的解集
的解集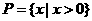 ,显然满足
,显然满足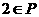 且
且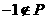 ,
,
即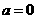 合乎题意;┅┅┅┅┅┅┅5分
合乎题意;┅┅┅┅┅┅┅5分
(2)当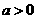 时,
时,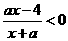 的解集
的解集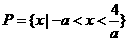 ,由于
,由于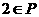 且
且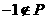 ,
,
则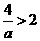 且
且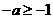 ,因此
,因此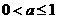 满足题设;┅┅┅┅┅┅┅7分
满足题设;┅┅┅┅┅┅┅7分
(3)当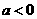 时,
时,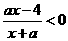 的解集
的解集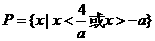 ,由于
,由于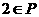 且
且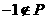 ,
,
则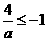 且
且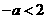 ,因此
,因此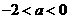 满足题设;┅┅┅┅┅┅┅9分
满足题设;┅┅┅┅┅┅┅9分
综上:实数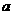 的取值范围为
的取值范围为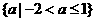 .┅┅┅┅┅┅┅10分
.┅┅┅┅┅┅┅10分
解法2:∵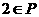 ,∴
,∴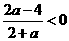 ,即
,即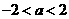 ,
, 

又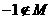 ,则
,则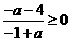 或
或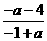 无意义,即
无意义,即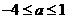 ,
,
因此实数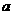 的取值范围为
的取值范围为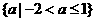 .
. 

16. 不合格 解:由于圆柱形零件的外径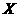 -N(4,0.25),由正态分布的特征可知,正态分布N(4,0.25)在区间(4-3×0.5,4+3×0.5)即(2.5,5.5)之外取值的概率只有0.003,而
-N(4,0.25),由正态分布的特征可知,正态分布N(4,0.25)在区间(4-3×0.5,4+3×0.5)即(2.5,5.5)之外取值的概率只有0.003,而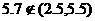 ,这说明在一次试验中,出现了几乎不可能发生的小概率事件,根据统计中假设检验的基本思想,认为该厂这批产品是不合格的。
,这说明在一次试验中,出现了几乎不可能发生的小概率事件,根据统计中假设检验的基本思想,认为该厂这批产品是不合格的。 

15.下列答案中任一即可,答案不唯一
(1从二面角的棱出发的一个半平面内任意一点到二面角的两个面的的距离之比为定值。
(2从二面角的棱上一点出发的一条射线上任意一点到二面角的两个面的的距离之比为定值。
(3)在空间,从角的顶点出发的一条射线上任意一点到角两边的距离之比为定值。
(4在空间,射线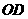 上任意一点
上任意一点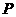 到射线
到射线 、
、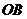 、
、 的距离之比不变。
的距离之比不变。
(5)在空间,射线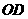 上任意一点
上任意一点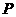 到平面
到平面 、
、 、
、 的距离之比不变。
的距离之比不变。
22. (本小题满分14分) 已知函数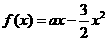 的最大值不小于
的最大值不小于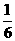 ,又当
,又当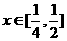 时,
时,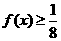 .
.
(I)求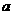 的值;
的值;


(II)设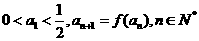 ,证明①
,证明①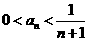 ;②若数列
;②若数列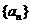 的前
的前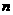 和为
和为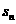 ,则
,则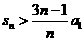
答案答案
21.(本小题满分12分)某房地产开发商投资81万元建一座写字楼,第一年装修费用为1万元,以后每年增加2万元,若把写字楼出租,则每年可以收入租金30万元.
(I)若扣除投资和装修费,则从第几年开始获取纯利润? 

(II)若干年后开发商为了投资其他项目,有两种处理方案:①纯利润总和最大时,以10万元出售;②该楼年平均利润最大时以46万元出售该楼,问哪种方案更优?
20.(本小题满分12分)已知平面内点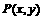 满足
满足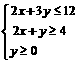 ,
,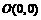 为坐标原点.请完成下列各问:
为坐标原点.请完成下列各问:
(I)若点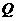 的坐标为(1,1),求目标函数
的坐标为(1,1),求目标函数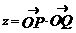 的最大值和最小值.
的最大值和最小值.
(II)是否存在实数 ,使得有无穷多个P点,使得目标函数
,使得有无穷多个P点,使得目标函数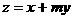 取得最小值,若存在,试求出
取得最小值,若存在,试求出 的值,若不存在请说明理由.
的值,若不存在请说明理由. 

19.(本小题满分12分) 甲、乙、丙三人分别独立的进行某项技能测试,已知甲能通过测试的概率是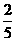 ,甲、乙、丙三人都能通过测试的概率是
,甲、乙、丙三人都能通过测试的概率是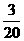 ,甲、乙、丙三人都不能通过测试的概率是
,甲、乙、丙三人都不能通过测试的概率是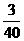 ,且乙通过测试的概率比丙大.
,且乙通过测试的概率比丙大.
(Ⅰ)求乙、丙两人各自通过测试的概率分别是多少; 

(Ⅱ)求测试结束后通过的人数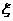 的数学期望
的数学期望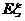 .
.
(III)求在乙通过测试的条件下,甲没有通过测试的概率.
18.(本小题满分10分)过点A(-2,4)引倾斜角为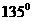 的直线,交曲线
的直线,交曲线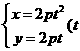 为参
为参
数,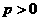 )于
)于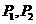 两点,若
两点,若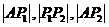 成等比数列,求
成等比数列,求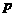 的值.
的值.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com