
题目列表(包括答案和解析)
5.二次函数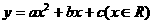 的部分对应值如下表:
的部分对应值如下表:
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
|
y |
6 |
0 |
-4 |
-6 |
-6 |
-4 |
0 |
6 |
则不等式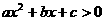 的解集是_________________.
的解集是_________________.
4. 对“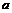 、
、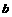 、
、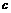 是不全相等的正数”,给出下列判断:
是不全相等的正数”,给出下列判断:
①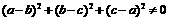 ; ②
; ②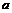 >
>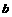 与
与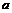 <
<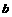 及
及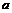 ≠
≠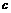 中至少有一个成立;
中至少有一个成立;
③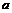 ≠
≠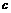 ,
,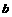 ≠
≠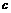 ,
,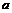 ≠
≠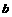 不能同时成立.其中判断正确的个数为 ( )
不能同时成立.其中判断正确的个数为 ( )
A.0个 B.1个 C.2个 D.3个
3.(2004•辽宁)对于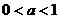 ,给出下列四个不等式 ( )
,给出下列四个不等式 ( )
①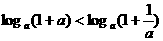 ②
②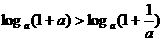
③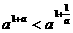 ④
④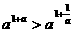
其中成立的是 ( )
A.①与③ B.①与④ C.②与③ D.②与④
2.(2004•湖北) 若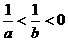 ,则下列不等式①
,则下列不等式①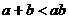 ;②
;②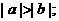 ③
③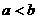 ;④
;④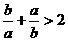 中,正确的不等式有 ( )
中,正确的不等式有 ( )
A.1个 B.2个 C.3个 D.4个
1.(2004•北京)已知a、b、c满足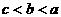 ,且
,且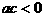 ,那么下列选项中不一定成立的是
,那么下列选项中不一定成立的是
( )
A.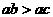 B.
B.
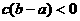 C.
C.
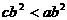 D.
D.
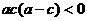
2.在运用不等式的性质是对不等式进行了非同解变形.
[基础演练]
1.不等式的“运算”只有加法法则和乘法法则,没有减法法则和除法法则,再利用数的性质进行转化时往往出错;
2.利用不等式的性质结合已知条件比较大小、判断不等式有关结论是否成立或利用不等式研究变量的范围,求字母的取值或取值范围等..如练习9.
[典例精析]
例1 : 若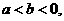 则下列不等式不能成立的是( )
则下列不等式不能成立的是( )
A. 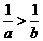 B.
B. 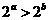
C. 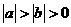 D.
D. 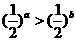
解析: 由
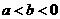 知 ab >0, 因此
知 ab >0, 因此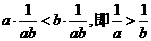 成立;
成立;
由
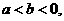 得
得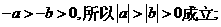
由于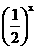 是减函数, 所以
是减函数, 所以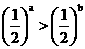 亦成立,故一定不成立的是B.
亦成立,故一定不成立的是B.
答案:B.
例2:(2003•北京)设a,b,c,d∈R,且a>b,c>d,则下列结论中正确的是( )
A.a+c>b+d B.a-c>b-d
C.ac>bd D.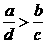
解析:∵a>b,c>d,∴a+c>b+D.
答案:A.
例3:(2005•福建)不等式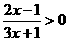 的解集是( )
的解集是( )
A.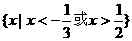 B.
B.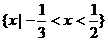
C.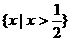 D.
D.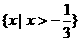
解析:不等式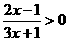 的解是x>
的解是x>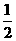 或x<
或x<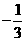 .
.
答案:A.
[常见误区]
1.不等式的性质主要以客观题形式出现往往融于其他问题之中,.如例1,例2
1.理解不等式的性质及其证明.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com