
题目列表(包括答案和解析)
2.下列有关命题的说法正确的是 ( ).
A.命题“若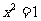 ,则
,则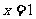 ”的否命题为:“若
”的否命题为:“若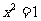 ,则
,则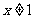 ”.
”.
B.“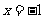 ”是“
”是“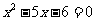 ”的必要不充分条件.
”的必要不充分条件.
C.命题“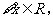 使得
使得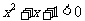 ”的否定是:“
”的否定是:“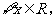 均有
均有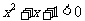 ”.
”.
D.命题“若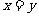 ,则
,则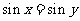 ”的逆否命题为真命题.
”的逆否命题为真命题.
1.已知集合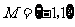 ,
,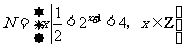 ,则
,则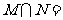 ( )
( )
A. B.
B.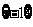 C.
C.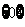 D.
D.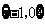
22.((本小题满分9分)2009浙江文))已知函数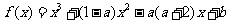
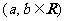 .
.
(I)若函数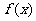 的图象过原点,且在原点处的切线斜率是
的图象过原点,且在原点处的切线斜率是 ,求
,求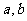 的值;
的值;
(II)若函数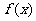 在区间
在区间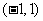 上不单调,求
上不单调,求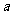 的取值范围.
的取值范围.
解析:(Ⅰ)由题意得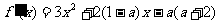
又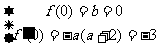 ,解得
,解得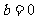 ,
,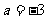 或
或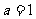
(Ⅱ)函数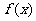 在区间
在区间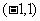 不单调,等价于
不单调,等价于
导函数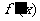 在
在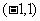 既能取到大于0的实数,又能取到小于0的实数
既能取到大于0的实数,又能取到小于0的实数
即函数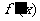 在
在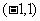 上存在零点,根据零点存在定理,有
上存在零点,根据零点存在定理,有
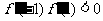 , 即:
, 即: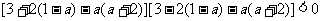
整理得: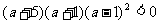 ,解得
,解得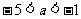
21.((本小题满分8分)2009四川卷文) 

已知椭圆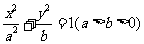 的左、右焦点分别为
的左、右焦点分别为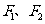 ,离心率
,离心率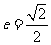 ,右准线方程为
,右准线方程为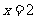 。
。
(I)求椭圆的标准方程;
(II)过点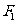 的直线
的直线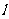 与该椭圆交于
与该椭圆交于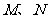 两点,且
两点,且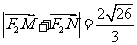 ,求直线
,求直线 的方程。
的方程。
[解析](I)由已知得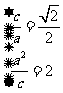 ,解得
,解得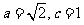


∴ 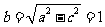
∴ 所求椭圆的方程为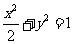
(II)由(I)得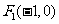 、
、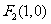
①若直线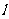 的斜率不存在,则直线
的斜率不存在,则直线 的方程为
的方程为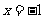 ,由
,由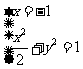 得
得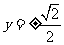
设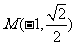 、
、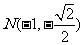 ,
, 

∴ 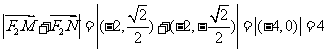 ,这与已知相矛盾。
,这与已知相矛盾。
②若直线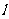 的斜率存在,设直线直线
的斜率存在,设直线直线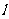 的斜率为
的斜率为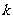 ,则直线
,则直线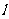 的方程为
的方程为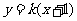 ,
,
设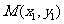 、
、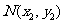 ,
,
联立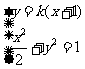 ,消元得
,消元得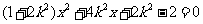
∴ 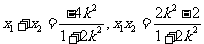 ,
, 

∴ 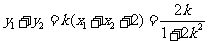 ,
, 

又∵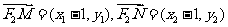
∴ 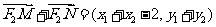
∴ 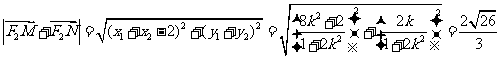
化简得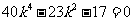
解得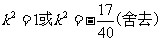
∴ 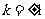
20.((本小题满分8分)2009湖北卷文)
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:元)。
(Ⅰ)将y表示为x的函数:
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
解:(1)如图,设矩形的另一边长为a m
则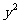 -45x-180(x-2)+180·2a=225x+360a-360
-45x-180(x-2)+180·2a=225x+360a-360
由已知xa=360,得a=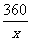 ,
,
所以y=225x+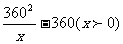


(II)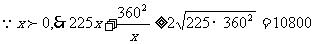
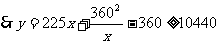 .当且仅当225x=
.当且仅当225x=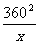 时,等号成立.
时,等号成立.
即当x=24m时,修建围墙的总费用最小,最小总费用是10440元.
19.((本小题满分8分)2009江西卷理)
设函数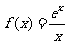
(1) 求函数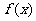 的单调区间;
的单调区间;
(2) 若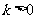 ,求不等式
,求不等式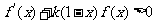 的解集.
的解集.
解: (1) 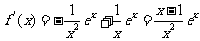 ,
由
,
由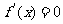 ,得
,得 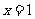 .
.
因为 当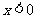 时,
时,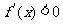 ;
当
;
当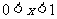 时,
时,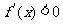 ;
当
;
当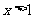 时,
时,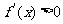 ;
;
所以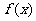 的单调增区间是:
的单调增区间是: ;
单调减区间是:
;
单调减区间是: 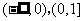 .
.
(2)
由 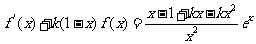
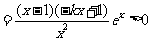 ,
,
得: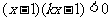 .
.
故:当
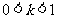 时, 解集是:
时, 解集是: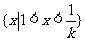 ;
;
当
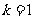 时,解集是:
时,解集是:
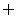 ;
;
当
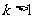 时, 解集是:
时, 解集是: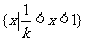 .
.
18.((本小题满分8分)2009江西卷文)若存在过点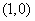 的直线与曲线
的直线与曲线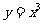 和
和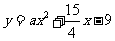 都相切,求
都相切,求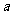 的值。
。
的值。
。
[答案]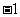 或
或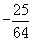
[解析]设过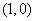 的直线与
的直线与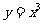 相切于点
相切于点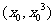 ,所以切线方程为
,所以切线方程为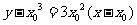
即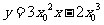 ,又
,又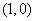 在切线上,则
在切线上,则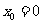 或
或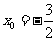 ,
,
当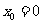 时,由
时,由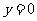 与
与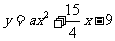 相切可得
相切可得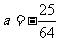 ,
,
当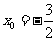 时,由
时,由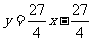 与
与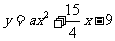 相切可得
相切可得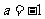 ,
,
17.((本小题满分7分)2009山东卷文)设斜率为2的直线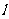 过抛物线
过抛物线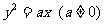 的焦点F,且和
的焦点F,且和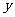 轴交于点A,若△OAF(O为坐标原点)的面积为4,
轴交于点A,若△OAF(O为坐标原点)的面积为4,
(1)求抛物线方程
(2)P为抛物线上的点,且PF=4,求点P的坐标。
[答案]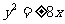
[解析]: (1)抛物线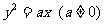 的焦点F坐标为
的焦点F坐标为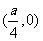 ,则直线
,则直线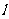 的方程为
的方程为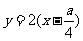 ,它与
,它与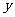 轴的交点为A
轴的交点为A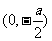 ,所以△OAF的面积为
,所以△OAF的面积为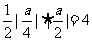 ,解得
,解得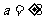 .所以抛物线方程为
.所以抛物线方程为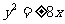 ,.
,. 
 (2)缺答案
(2)缺答案
15.(2009安徽卷理)若不等式组 所表示的平面区域被直线
所表示的平面区域被直线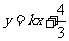 分为面积相等的两部分,则
分为面积相等的两部分,则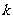 的值是 .
的值是 .
[答案]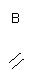
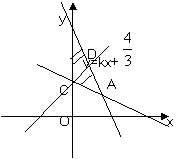 [解析]:不等式表示的平面区域如图所示阴影部分△ABC
[解析]:不等式表示的平面区域如图所示阴影部分△ABC
由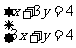 得A(1,1),又B(0,4),C(0,
得A(1,1),又B(0,4),C(0,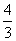 )
)
∴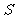 △ABC=
△ABC=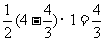 ,设
,设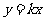 与
与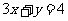 的
的
交点为D,则由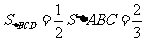 知
知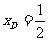 ,∴
,∴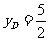
∴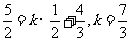 选填
选填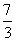 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com