
题目列表(包括答案和解析)
5.把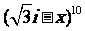 用二项式定理展开,展开式的第4项的系数是
用二项式定理展开,展开式的第4项的系数是
A.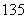 B.
B.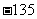 C.
C. D.
D.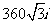
4.设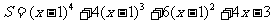 ,则S等于
,则S等于
A.x4 B.x4+1 C.(x-2)4 D.x4+4
3.袋中有5个黑球和3个白球,从中任取2个球,则其中至少有1个黑球的概率是
A.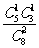 B.
B. C.
C.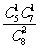 D.
D.
2.从装有2个红球和2个白球的口袋中任取2个球,其中互斥而不对立的两个事件是
A.“至少有1个白球”与“都是白球”
B.“恰有1个白球”与“恰有2个红球”
C.“至少有1个白球”与“都是红球”
D.“至多有1个白球”与“至少有1个红球”
1.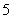 个人排成一排,其中甲、乙两人至少有一人在两端的排法种数有
个人排成一排,其中甲、乙两人至少有一人在两端的排法种数有
A.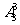 B.
B.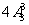
C.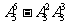 D.
D.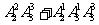
21.(本小题满分14分)设函数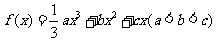 ,其图象对应的曲线设为G.
,其图象对应的曲线设为G.
(Ⅰ)设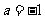 、
、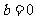 、
、 ,
, 为经过点(2,2)的曲线G的切线,求
为经过点(2,2)的曲线G的切线,求 的方程;
的方程;
(Ⅱ)已知曲线G在点A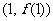 、B
、B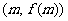 处的切线的斜率分别为0、
处的切线的斜率分别为0、 ,求证:
,求证: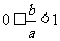 ;
;
(Ⅲ)在(Ⅱ)的条件下,当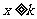 时,
时,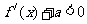 恒成立,求常数
恒成立,求常数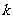 的最小值.
的最小值.
[解答](Ⅰ)由题设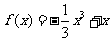 ,∴
,∴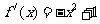 ,
,
由于点(2,2)不在曲线G上,
可设切点为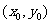 ,所求切线方程为
,所求切线方程为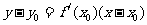 ,
,
由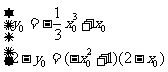 ,消去
,消去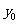 得
得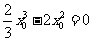 ,
, 

∴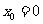 ,或
,或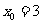 ,即对应的切点为(0,0),或
,即对应的切点为(0,0),或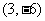 ,
,
当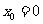 时,
时,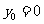 ,
,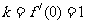 ,所求的切线方程为
,所求的切线方程为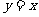 , …………2分
, …………2分
当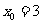 时,
时, ,
,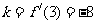 ,所求切线方程为
,所求切线方程为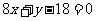 ;…4分
;…4分
(Ⅱ)由已知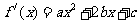 ,依题意有
,依题意有
 ,
,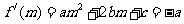 ,即
,即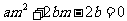 ,
,
从而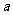 、
、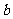 、
、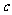 三数中至少有一个正数一个负数,∴总有
三数中至少有一个正数一个负数,∴总有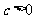 ,
,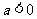 ,
,
若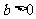 ,由
,由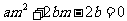 有
有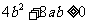 ,
,
∴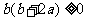 ,∴
,∴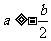 ,
, 

又 ,∴
,∴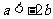 ,
,
故得 ,从而
,从而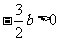 ,
,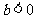 矛盾,
矛盾,
∴必有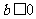 ,∴
,∴
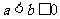 ,∴可得
,∴可得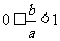 ; …………8分
; …………8分
(Ⅲ)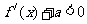 即
即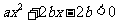 ,
,
整理即得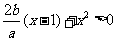 ,设
,设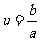 ,则
,则
设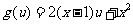 为
为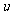 的函数,由条件(Ⅱ),
的函数,由条件(Ⅱ),
欲不等式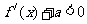 恒成立,即
恒成立,即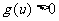 在
在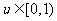 时恒成立,
时恒成立,
∴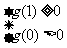 ,∴
,∴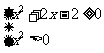 ,
,
解得 ,或
,或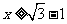 ,
, 

依题意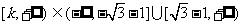 ,
,
∴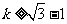 ,即所求的
,即所求的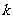 的最小值为
的最小值为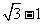 . …………14分
. …………14分
本题综合考查曲线的概念、一次函数的性质、导数的几何意义、不等式的解法与证明,属难题.

20.(本小题满分12分)已知
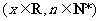 ,设
,设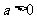 ,
,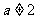 .
.
(Ⅰ)求出函数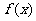 的解析式;
的解析式;
(Ⅱ)是否存在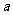 使得函数
使得函数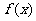 能以
能以 为其最小值?若能,求出对应的
为其最小值?若能,求出对应的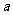 的取值或取值范围;若不能,试说明理由.
的取值或取值范围;若不能,试说明理由.
[解答](Ⅰ)∵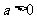 ,
,
∴当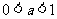 时
时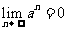 ,
, 

∴ ,
,
此时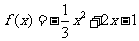 ,函数图象开口向下,没有最小值; …………3分
,函数图象开口向下,没有最小值; …………3分
当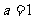 时,
时,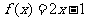 ,函数单调递增,此时也没有最小值; …………5分
,函数单调递增,此时也没有最小值; …………5分
当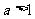 且
且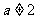 时
时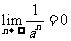 ,
,
∴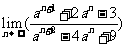



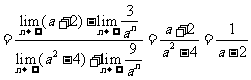 ,
,
此时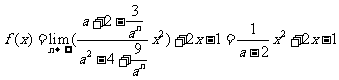 ; …………8分
; …………8分
(Ⅱ)若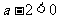 即
即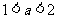 时,函数
时,函数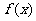 开口向下,没有最小值,
开口向下,没有最小值,
而当 即
即 时,函数
时,函数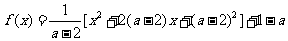 ,
,
当且仅当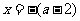 时有最小值
时有最小值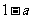 ,
, 

令 ,则
,则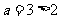 ,
,
∴存在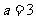 恰使函数
恰使函数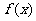 以
以 为其最小值. …………12分
为其最小值. …………12分
本题考查极限的概念、数列极限的求法、重要极限的应用、二次函数的最值及分类讨论的思想方法,属易错题、难题
19.(本小题满分13分)随着石油资源的日益紧缺,我国决定建立自己的石油储备基地,
已知某石油储备基地原储有石油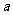 吨,按计划正式运营后的第一年进油量为已储油量的25%,以后每年的进油量均为上一年底储油量的25%,且每年年内用出
吨,按计划正式运营后的第一年进油量为已储油量的25%,以后每年的进油量均为上一年底储油量的25%,且每年年内用出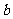 吨,设
吨,设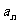 为正式运营后第
为正式运营后第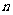 年年底的石油储量.
年年底的石油储量.
(Ⅰ)求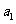 、
、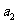 、
、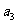 ;
;
(Ⅱ)猜测出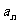 的表达式并用数学归纳法予以证明;
的表达式并用数学归纳法予以证明;
(Ⅲ)为抵御突发事件,该油库年底储油量不得少于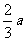 吨,如果
吨,如果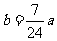 吨,该油库能否长期按计划运营?如果能,请加以证明;如果不能,请说明理由.
吨,该油库能否长期按计划运营?如果能,请加以证明;如果不能,请说明理由.
(计算中可供参考的数据: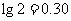 ,
,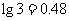 )
)
[解答](Ⅰ)依题意,油库原有储油量为a吨,则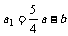 ,
,
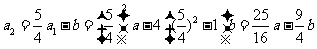 ,
,
 ,…; …………3分
,…; …………3分
(Ⅱ)由(Ⅰ)猜测:对于任意正整数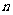 恒有
恒有
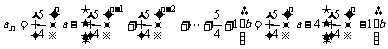 ,
,
下用数学归纳法证明:
1o当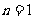 时,
时,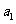
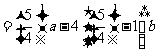
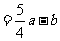 ,猜测成立; …………4分
,猜测成立; …………4分
2o假设当 时,
时,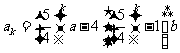 成立, …………5分
成立, …………5分
那么,由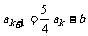 ,得
,得



 ,
,
这就是说当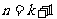 时,猜测也成立,
时,猜测也成立,
综合1o、2o知,对于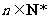 猜测都成立; …………8分
猜测都成立; …………8分
(Ⅲ)如果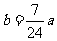 吨时,该油库第
吨时,该油库第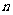 年年底的储油量不少于
年年底的储油量不少于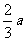 吨,
吨,
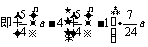
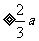 ,∴
,∴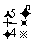 ≤3, …………10分
≤3, …………10分
∴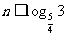 =
=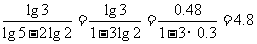 ,
, 

说明该油库只能在5年内运营,因此不能长期运营. …………13分
本题考查数列知识、数学归纳法的应用、不等式的解法和数学应用能力,属较难题.
18.(本小题满分12分)已知高二年级的某6名学生,独立回答某类问题时答对的概率都是0.5,而将这6名同学平均分为甲、乙、丙3个小组后,每个小组经过两名同学讨论后再回答同类问题时答对此类问题的概率都是0.7,若各个同学或各个小组回答问题时都是相互独立的.
(Ⅰ)这6名同学平均分成3组,共有分法多少种?
(Ⅱ)若分组后,3个小组中恰有2组能答对此类问题的概率是多少?
(Ⅲ)若要求独立回答,则这6名学生中至多有4人能答对此类问题的概率是多少?
[解答](Ⅰ)所求的方法数是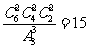 ; …………4分
; …………4分
(Ⅱ)由独立重复试验知,这3个小组中恰有2组答对此类问题的概率
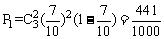 ; …………8分
; …………8分
(Ⅲ)由对立事件的概率,至多4人答对此类问题的概率为1减去至少5人答对此类问题的概率,即
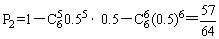 . …………12分
. …………12分
本题考查均匀分组问题、相互独立事件同时发生的概率、对立事件的概率加法公式,属基本题
17.(本小题满分12分)设二项式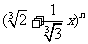
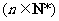 的展开式中第7项的系数与倒数第7项的系数之比是
的展开式中第7项的系数与倒数第7项的系数之比是 .
.
(Ⅰ)求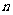 ;
;
(Ⅱ)展开式中有多少项的系数是有理数,指出它们分别是哪几项.
[解答](Ⅰ)第7项即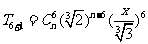 ,
,
而倒数第7项即二项式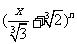 的第7项,也即
的第7项,也即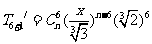 ,
,
依题意有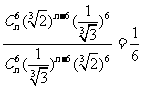 ,化简得
,化简得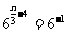 ,∴
,∴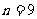 ; …………6分
; …………6分
(Ⅱ)展开式的通项为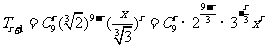 ,
,
欲对应项的系数是有理数,则 和
和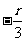 都为整数,
都为整数,
注意到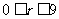 ,
, ,∴
,∴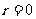 、3、6、9,
、3、6、9,
即系数为有理数的项分别是第1项、第4项、第7项和第10项. …………12分
(它们分别为: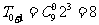 ,
,
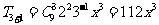 ,
,
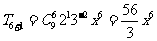 ,
,
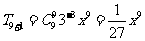 ,两种结果同样得满分)
,两种结果同样得满分)
本题考查二项式定理、二项式系数与系数的概念、二项式定理的通项的应用,属基本题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com