3.两个计数原理的区别:

如果完成一件事，有n类办法，不论哪一类办法中的哪一种方法，都能独立完成这件事,用分类计数原理，

如果完成一件事需要分成几个步骤，各步骤都不可缺少，需要完成所有步骤才能完成这件事，是分步问题,用分步计数原理.

两个计数原理用来计算完成一件事的不同方法种数的，是计算排列组合,概率统计的基础,在生产,生活及科学实验中有广泛的应用.

2.分步计数原理：做一件事情，完成它需要分成n个步骤，做第一步有m₁种不同的方法，做第二步有m₂种不同的方法，……，做第n步有m_n种不同的方法，那么完成这件事有N=m₁×m₂×……m_n 种不同的方法

1.分类计数原理：做一件事情，完成它可以有n类办法，在第一类办法中有m₁种不同的方法，在第二类办法中有m₂种不同的方法，……，在第n类办法中有m_n种不同的方法那么完成这件事共有

　N=m₁+m₂+……+m_n 种不同的方法

1理解分类计数原理与分步计数原理，并能用它们分析和解决一些简单的应用问题;

2.理解排列的意义;掌握排列数计算公式，并能用它解决一些简单的应用问题.

10.如果在(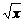+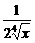)ⁿ的展开式中，前三项系数成等差数列，求展开式中的有理项.

8. (2005广东)已知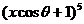的展开式中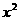的系数与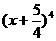的展开式中x³的系数相等，则=　　　　　　　 .

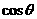7.(2005浙江)在(1－x)⁵+(1－x)⁶+(1－x)⁷+(1－x)⁸的展开式中，含x³的项的系数是_____

6.(2005山东)如果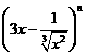的展开式中各项系数之和为128，则展开式中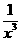的系数是________

5.(2006北京)在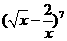的展开式中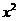，的系数是__________(用数字作答).

4.一串装饰彩灯由灯泡串联而成，每串有20个灯泡，只要有一只灯泡坏了，整串灯泡就不亮，则因灯泡损坏致使一串彩灯不亮的可能性的种数为　 (　 )

A.20　　　　　　 　　　 B.2¹⁹ C.2²⁰ D.2²⁰－1