
题目列表(包括答案和解析)
2.集合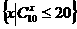 中元素个数为( )
中元素个数为( )
A.2个 B.3个 C.4个 D.5个
1. 某公司共有1000名员工,下设若干部门,现采用分层抽样方法,从全体员工中抽取一个容量为80的样本,已知广告部被抽取了4个员工,则广告部的员工人数是( )
A. 30 B.40 C.50 D.60
22.(1) 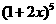 的二项式系数和为_______
的二项式系数和为_______
(2)某工厂建造一个容积为8 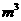 ,深为2
,深为2  的长方体无盖水池,如果池底和池壁的造价分别为120元/
的长方体无盖水池,如果池底和池壁的造价分别为120元/  和80元/
和80元/  ,那么水池的最低造价为多少元?(
,那么水池的最低造价为多少元?(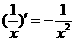 )
)


21.(满分16分)下表为某班英语及数学成绩的分布.学生共有50人,成绩分1~5五个档次.例如表中所示英语成绩为4分、数学成绩为2分的学生为5人.将全班学生的姓名卡片混在一起,任取一枚,该卡片同学的英语成绩为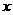 ,数学成绩为
,数学成绩为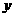 .设
.设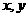 为随机变量(注:没有相同姓名的学生).
为随机变量(注:没有相同姓名的学生). 

(Ⅰ)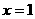 的概率为多少?
的概率为多少? 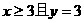 的概率为多少?
的概率为多少?
(Ⅱ)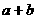 等于多少?
等于多少?
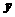 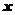 |
数学 |
|||||
|
5 |
4 |
3 |
2 |
1 |
||
|
英语 |
5 |
1 |
3 |
1 |
0 |
1 |
|
4 |
1 |
0 |
7 |
5 |
1 |
|
|
3 |
2 |
1 |
0 |
9 |
3 |
|
|
2 |
1 |
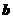 |
6 |
0 |
 |
|
|
1 |
0 |
0 |
1 |
1 |
3 |
20. (满分14分)已知f(x)=ax3+bx2+cx(a≠0)在x=±1时取得极值,
且f(1)=-1.
(1)试求常数a、b、c的值;
(2)试判断x=±1是函数的极小值还是极大值,并说明理由;
(3)求函数f(x) 在[-3,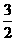 ]上的最大值与最小值。
]上的最大值与最小值。 

19.(满分14分)如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1是菱形,四边形BCC1B1是矩形,AB⊥BC,CB=3,AB=4,∠A1AB=60°。
|
|


|
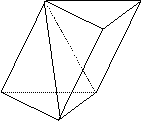 (2)求直线A1C与平面BCC1B所成角的正切值;
(2)求直线A1C与平面BCC1B所成角的正切值;
(3)求点C1到平面A1CB的距离。
|
|
|
18.(满分14分)蚂蚁A位于数轴x=0处,蚂蚁B位于x=2处, 这两只蚂蚁每隔一秒钟向左或向右移动一个单位,设它们向右移动的概率为 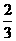 ,向左移动的概率为
,向左移动的概率为 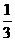 。
。
(1)求3秒后,蚂蚁A在x=1处的概率;
(2)求4秒后,蚂蚁A、B同时在x=2处的概率。 

17.(满分12分)已知函数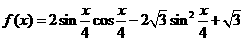 .
.
(Ⅰ)求函数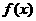 的最小正周期及最值;
的最小正周期及最值;
(Ⅱ)令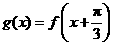 ,判断函数
,判断函数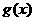 的奇偶性,并说明理由.
的奇偶性,并说明理由. 

15.设P、A、B、C是球O表面上的四点,且PA、PB、PC两两互相垂直,若PA=PB=PC=a, 则球心O到截面ABC的距离是______________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com