
题目列表(包括答案和解析)
1.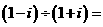
A.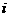 B.
B.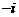 C.
C.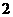 D.
D.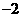
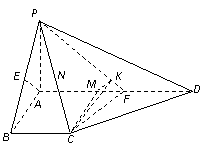
21.(本小题满分14分)如图,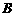 为等腰直角
为等腰直角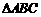 的直角顶点,
的直角顶点,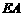 、
、 都垂直于
都垂直于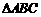
所在的平面,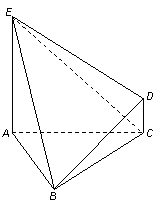
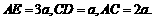
(1)求二面角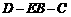 的大小;
的大小;
(2)求点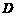 到平面
到平面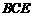 的距离;
的距离;
(3)问线段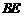 上是否存在一点
上是否存在一点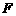 ,使得
,使得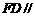 平面
平面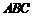 且
且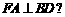 若存在,请指出
若存在,请指出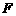 点的位置;若不存在,请说明理由.
点的位置;若不存在,请说明理由.
答案:几何法:
(1)作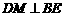 于
于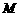 ,
,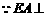 平面
平面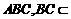 平面
平面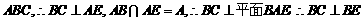
则向量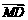 与
与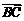 所成的角即为二面角
所成的角即为二面角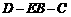 的大小.
的大小.
由计算得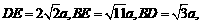 故
故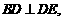
∴由面积求得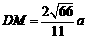 ,由射影定理可求得
,由射影定理可求得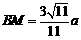 .
.
而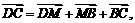 则
则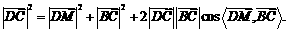
 故
故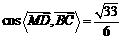 ,故二面角
,故二面角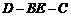 的大小为
的大小为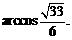
(2)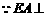 平面
平面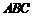 ,
,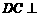 平面
平面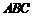 ,
,
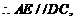 故A、C、D、E四点共面. 且平面
故A、C、D、E四点共面. 且平面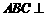 平面
平面
作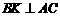 于
于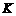 ,则有
,则有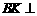 平面
平面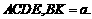
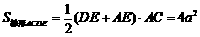 ,
,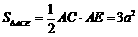
∴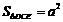 ∴
∴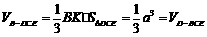
由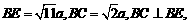 故
故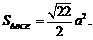
由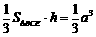 得
得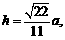 即
即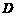 到平面
到平面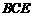 的距离是
的距离是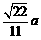 .
.
(3)假设线段BE上存在点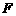 ,使
,使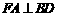 ,
,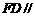 平面
平面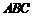 .
.
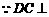 平面
平面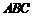 ,
,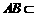 平面
平面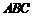 .
.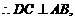 又
又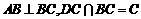 ,
,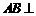 平面
平面
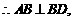 又
又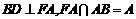 (F不与B重合),故
(F不与B重合),故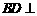 平面
平面 ,则
,则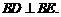
而由计算得: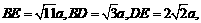 故
故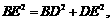
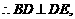 这与
这与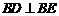 矛盾,故
矛盾,故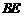 上不存在
上不存在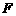 ,使
,使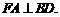 (或
(或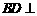 平面
平面 ,
,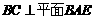 ,而过空间一点有且仅有一条直线与已知平面垂直)
,而过空间一点有且仅有一条直线与已知平面垂直)
向量法:
过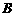 作
作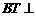 平面
平面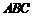 ,以
,以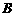 为坐标原点,建立如图所示的空间直角坐标系,则
为坐标原点,建立如图所示的空间直角坐标系,则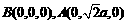 ,
,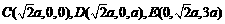 .
.
(1)设平面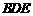 的一个法向量为
的一个法向量为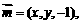 则
则 ,
,
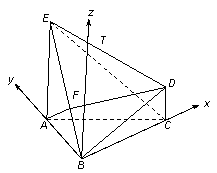 故
故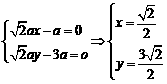
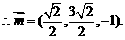
同理:平面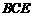 的一个法向量为
的一个法向量为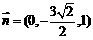 ,则
,则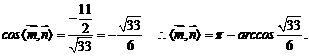
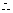 二面角
二面角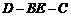 的大小为
的大小为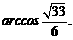
(2)由(1)知平面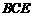 的一个法向量为
的一个法向量为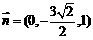 ,而
,而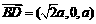 ,
,
故D到平面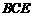 的距离是
的距离是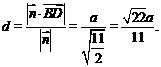
(3)若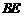 上存在
上存在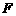 使
使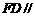 平面
平面 ,显然此时
,显然此时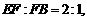 故
故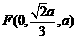
(上式也可用向量共线与共面定理得到F点的坐标)∴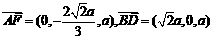 ,
,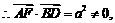 故
故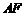 与
与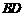 不垂直,故在
不垂直,故在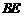 上不存在符合题意的
上不存在符合题意的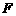 点。
点。
 (3)若点F存在,则
(3)若点F存在,则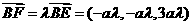 ,
,
由B(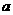 ,0,0),∴F
,0,0),∴F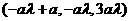 ,
,
∴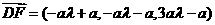 ,
,
平面ABC的法向量是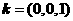 ,
,
由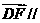 平面ABC,∴
平面ABC,∴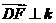 ,
,
∴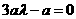 ,∴
,∴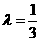 ,即F
,即F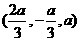 ,
,
∴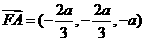 ,
,
而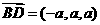 ,欲
,欲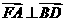 ,∴
,∴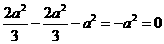 ,
,
这不可能,∴这样的点F不存在。
20.(本小题满分13分)如图,在梯形 中,
中,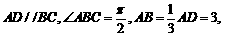
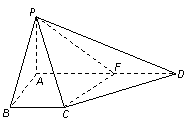
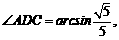
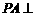 平面
平面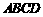 ,且
,且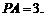
(1)求异面直线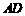 与
与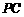 间的距离;
间的距离;
(2)求直线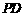 与平面
与平面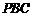 所成的角;
所成的角;
(3)已知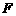 是线段
是线段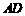 上的动点,若二面角
上的动点,若二面角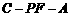 的
的
大小为 ,求AF.
,求AF.
答案:(1)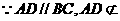 平面
平面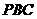
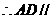 平面
平面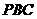 ,故
,故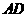 与
与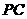 间的距离就是
间的距离就是
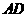 到平面
到平面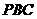 的距离.取
的距离.取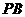 中点
中点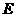 ,连
,连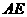 .
.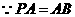
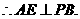
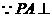 平面
平面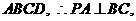 又
又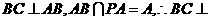 平面
平面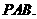 故平面
故平面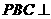 平面
平面 由
由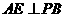 得
得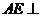 平面
平面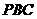 ,故
,故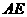 的长度是
的长度是 到平面
到平面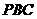 的距离,而
的距离,而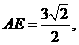 故
故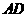 与
与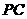 间的距离是
间的距离是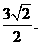
 (2)由(1)知:
(2)由(1)知: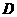 到平面
到平面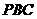 的距离即为
的距离即为 到平面
到平面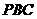 距离,故
距离,故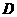 到平面
到平面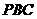 的距离是
的距离是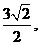 在
在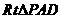 中:
中: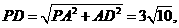 设直线
设直线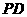 与平面
与平面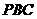 所成的角是
所成的角是 ,故
,故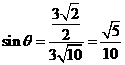 ,∴直线
,∴直线 与平面
与平面 所成的角是
所成的角是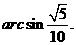
(3)作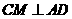 于
于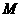 ,作
,作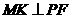 于
于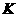 ,连
,连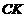 .由
.由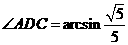 得
得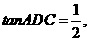 则
则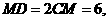 证得
证得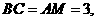 可证
可证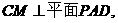 得∠CKM是二面角
得∠CKM是二面角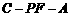 的平面角,所以
的平面角,所以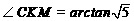 ,
,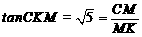 ,
,
∴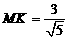 ,由
,由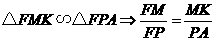 ,
,
设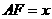 ,则
,则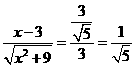 ,
,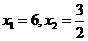 ,由二面角
,由二面角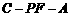 的平面角小于
的平面角小于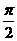 得
得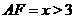 ,故取
,故取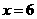 ,即
,即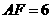 .
.
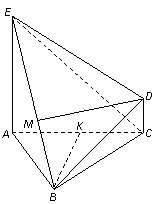
方法二:以A点为原点建立如图所示的空间直角坐标系,
使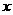 轴、
轴、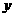 轴和
轴和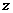 轴的正半轴依次过点B、D、P,则各点的坐标依次为
轴的正半轴依次过点B、D、P,则各点的坐标依次为
A(0,0,0)、B(3,0,0),C(3,3,0),D(0,9,0),P(0,0,3),
(Ⅰ)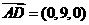 ,
,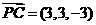 ,设
,设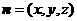 ,
,
则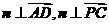 ,∴
,∴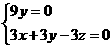 ,∴可取
,∴可取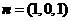 ,
,
而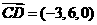 ,∴所求的距离
,∴所求的距离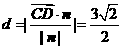 ;
;
(Ⅱ)设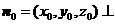 平面PBC,则由
平面PBC,则由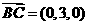 ,
,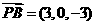 ,
,
∴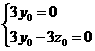 ,∴
,∴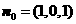 ,而
,而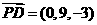 ,
,
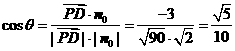 ,
,
∴所求的角为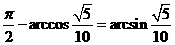 ;
;
(Ⅲ)设F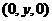 ,平面PAF的法向量是
,平面PAF的法向量是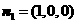 ,
,
设平面PCF的法向量是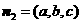 ,则
,则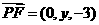 ,
,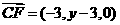 ,
,
∴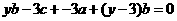 ,取
,取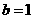 ,
,
∴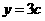 ,即
,即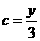 ,
,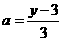 ,即
,即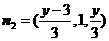 ,
,
∴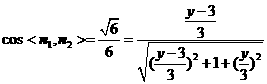 ,解得
,解得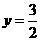 ,或
,或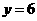 ,
,
但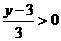 ,∴
,∴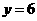 。
。
19.(本小题满分12分)号码为1、2、3、4、5、6的六个大小相同的球,放入编号为1、2、3、4、5、6的六个盒子中,每个盒子只能放一个球.
(1)若1、2号球要放入号码是相邻数字的两个盒子中,则不同的放法有多少种?
(2)若3、4号球要放入编号不比自己号码小的盒子中,则不同的放法有多少种?
(3)若1号球不放入1号盒中,6号球不放入6号盒中,则不同的放法有多少种?
答案:(1)号码是相邻数字的两个盒子有1与2、2与3、3与4、4与5、5与6共5种情况,则符合题意的放法有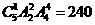 种;
种;
(2)①若3号球放入3号盒子,则不同的放法有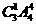 种;
种;
②若3号球放入4号、5号、6号盒子中的一个,则不同的放法有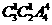 种;
种;
故符合题意的放法有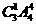 +
+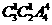 =216种;
=216种;
(3)六个球放入六个盒子中的方法有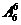 种,1号球放入1号盒中,6号球不放入6号盒中的方法有
种,1号球放入1号盒中,6号球不放入6号盒中的方法有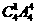 种;1号球不放入1号盒中,6号球放入6号盒中的方法有
种;1号球不放入1号盒中,6号球放入6号盒中的方法有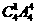 种;1号球放入1号盒中,6号球放入6号盒中的方法有
种;1号球放入1号盒中,6号球放入6号盒中的方法有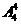 种;
种;
故符合题意的放法有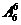 -
-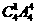 ×2-
×2-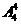 =504种.
=504种.
18.(本小题满分12分)如图,四边形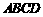 是边长为
是边长为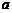 的正方形,
的正方形,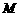 、
、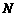 分别是边
分别是边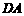 、
、
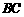 上的点(M不与A、D重合),且
上的点(M不与A、D重合),且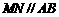 ,
, 交
交 于点
于点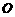 ,沿
,沿 将正方形折成
将正方形折成
直二面角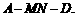
(1)当 平行移动时,
平行移动时, 的大小是否发生变化?试说明理由;
的大小是否发生变化?试说明理由;
(2)当 在怎样的位置时,
在怎样的位置时,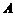 、
、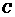 两点间的距离最小?并求出这个最小值.
两点间的距离最小?并求出这个最小值.
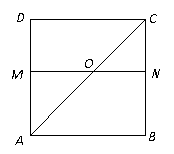

答案:(1)设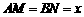 ,则
,则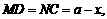 由题意知:平面
由题意知:平面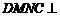 平面
平面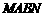 ,
,
而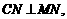 故
故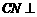 平面
平面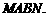
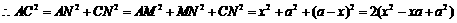 .
.
而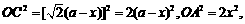 故
故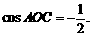
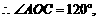
即无论 怎样平移,
怎样平移,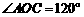 为定值.
为定值.
(2)由(1)知: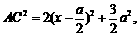 故当
故当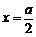 时,
时, 有最小值,即当M、N分别为
有最小值,即当M、N分别为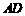 、
、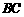 中点时,
中点时, 有最小值
有最小值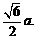
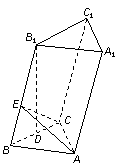
17.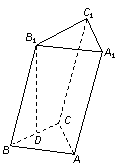 (本小题满分12分)如图,斜三棱柱
(本小题满分12分)如图,斜三棱柱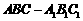 中,
中,
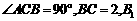 在底面的射影
在底面的射影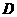 恰好是
恰好是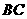 的中点,侧棱与底面
的中点,侧棱与底面
成 角,侧面
角,侧面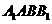 与侧面
与侧面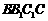 成
成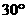 角.
角.
(1)求证:四边形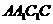 是矩形;
是矩形;
(2)求斜三棱柱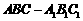 的体积.
的体积.
答案:(1)由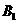 在底面的射影是
在底面的射影是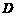 得
得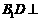 底面
底面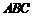 ,则
,则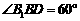 .
.
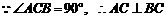 ,
,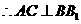 ,由
,由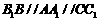 ,得四边形
,得四边形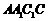 是矩形.
是矩形.
(2)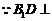 平面
平面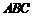 ,
, 侧面
侧面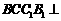 平面
平面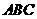 ,
,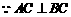 ,
, 侧面
侧面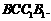
 过
过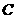 作
作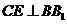 于
于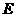 ,连
,连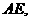 则
则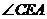 是侧面
是侧面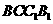 与侧面
与侧面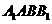 所成的二面角的平面角,故
所成的二面角的平面角,故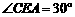 .
.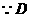 是
是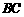 的中点,∴
的中点,∴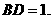 在
在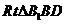 中,
中,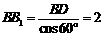 ,
,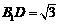 .在
.在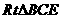 中,
中, 在
在 中,
中,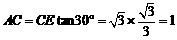 ,
, 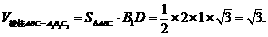
16.(本小题满分12分)已知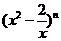 展开式的二项式系数之和比
展开式的二项式系数之和比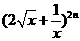 展开式的二项式系数之和小
展开式的二项式系数之和小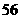 .
.
(1)求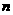 ;
;
(2)求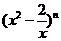 的第二项的系数和
的第二项的系数和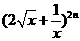 的第
的第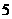 项.
项.
答案:(1)由题意得: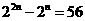 ,即
,即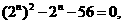 ∴
∴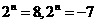 (舍去),故
(舍去),故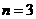 ;
;
(2) 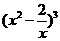 第二项是
第二项是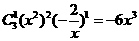 ,故第二项的系数是
,故第二项的系数是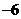 ;
;
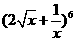 的第
的第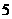 项是
项是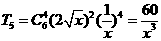 .
.
15.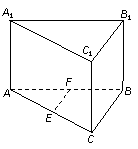 如图,在直棱柱
如图,在直棱柱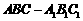 中,
中,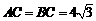 ,
,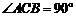 ,AA1=2,E、F分别是AC、AB的中点,过直线EF作棱柱的截面,若截面与平面ABC所成的二面角的大小为
,AA1=2,E、F分别是AC、AB的中点,过直线EF作棱柱的截面,若截面与平面ABC所成的二面角的大小为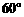 ,则截面的面积为____________.
,则截面的面积为____________.
答案: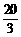 或
或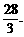 理由:由判断得经过A1或B1C1的截面与底面ABC
理由:由判断得经过A1或B1C1的截面与底面ABC
所成的角小于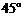 ,故截面与
,故截面与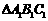 相交,且有两种情况:
相交,且有两种情况:
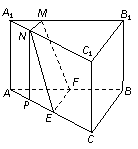 如图,截面为EFMN,过N作NP∥AA1,则NP⊥AC,
如图,截面为EFMN,过N作NP∥AA1,则NP⊥AC,
可证EF⊥平面A1C,则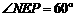 ,
,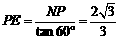 ,
,
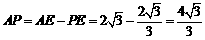 ,
,
故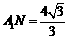 ,
,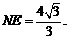 ∴
∴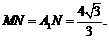
∴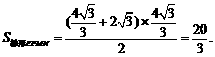
同理: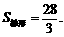 故截面面积为
故截面面积为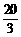 或
或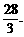
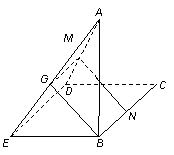
14.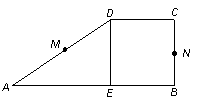 设M、N是直角梯形ABCD两腰的中点,DE⊥AB于E (如图). 现将
设M、N是直角梯形ABCD两腰的中点,DE⊥AB于E (如图). 现将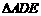 沿DE折起,使二面角
沿DE折起,使二面角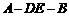 的大小为
的大小为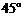 ,此时点A在平面BCDE内的射影恰为点B,则M、N的连线与AE所成角的大小为
.
,此时点A在平面BCDE内的射影恰为点B,则M、N的连线与AE所成角的大小为
.
 答案:
答案: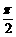 . 理由:
. 理由:
取AE中点G,连MG、GB. 则可证GM∥BN,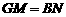
故MN∥BG,而DE⊥EB,DE⊥AE,∴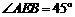
又AB⊥BE,G为AE中点,∴BG⊥AE, ∴MN⊥AE
∴MN与AE所成的角为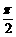 .
.
13.如果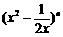 的展开式中只有第4项的二项式系数最大,则展开式中的所有项系数和是
.
的展开式中只有第4项的二项式系数最大,则展开式中的所有项系数和是
.
答案: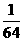 . 理由:由只有第4项的二项式系数最大得
. 理由:由只有第4项的二项式系数最大得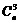 最大,故n=6. 令
最大,故n=6. 令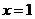 得展开式中所有项系数的和是
得展开式中所有项系数的和是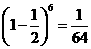 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com